Cho tam giác ABC đều, có H là trực tâm. Khẳng định nào sau đây sai?
\(\left(\overrightarrow{AH},\overrightarrow{BC}\right)=90^o\) \(\left(\overrightarrow{HC},\overrightarrow{HB}\right)=120^o\) \(\left(\overrightarrow{HA},\overrightarrow{HB}\right)=60^o\) \(\left(\overrightarrow{AH},\overrightarrow{HC}\right)=60^o\) Hướng dẫn giải: 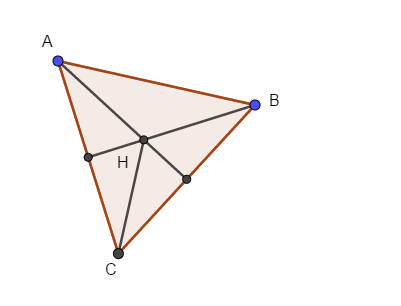
Vì H là trực tâm cũng là tâm đường tròn ngoại tiếp tam giác đêỳ ABC nên:
- AH là đường cao tam giác ABC, do đó \(AH\perp BC\Rightarrow\)\(\left(\overrightarrow{AH},\overrightarrow{BC}\right)=90^o\)
- H nhìn 3 cạnh tam giác dưới cùng một góc \(120^0\) nên \(\left(\overrightarrow{HC},\overrightarrow{HB}\right)=120^o\), \(\left(\overrightarrow{HA},\overrightarrow{HB}\right)=120^o\) suy ra " \(\left(\overrightarrow{HA},\overrightarrow{HB}\right)=60^o\)" là khẳng định sai.

