Các câu hỏi tương tự
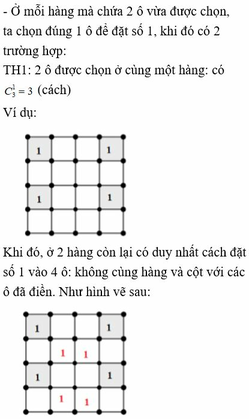
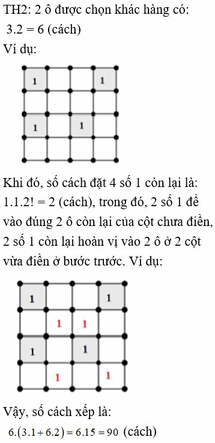
Xét bảng ô vuông gồm 4 x 4 ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số 1 hoặc -1 sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách? A. 72 B. 90 C. 80 D. 144
Đọc tiếp
Xét bảng ô vuông gồm 4 x 4 ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số 1 hoặc -1 sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách?
A. 72
B. 90
C. 80
D. 144
Cho một bảng ô vuông 3x3 Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng: A. P(A)
1
3
B. P(A)
5
7
C. P(A)
1
56
D. P(A)
10
21
Đọc tiếp
Cho một bảng ô vuông 3x3
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:
A. P(A) = 1 3
B. P(A) = 5 7
C. P(A) = 1 56
D. P(A) = 10 21
Cho một bảng ô vuông 3 × 3. Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
Đọc tiếp
Cho một bảng ô vuông 3 × 3.
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
![]()
![]()
![]()
![]()
Cho một bảng ô vuông 3x3. Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên ( mỗi ô chỉ điền một số). Gọi A là biến cố: “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng:
Đọc tiếp
Cho một bảng ô vuông 3x3. Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên ( mỗi ô chỉ điền một số). Gọi A là biến cố: “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng:
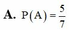
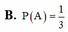
![]()
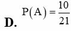
Cho một bảng ô vuông 3x3. Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng A. P(A)
1
3
B. P(A)
10
21
C. P(A)
5
7
D. P(A)
1
56
Đọc tiếp
Cho một bảng ô vuông 3x3.
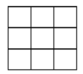
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
A. P(A) = 1 3
B. P(A) = 10 21
C. P(A) = 5 7
D. P(A) = 1 56
Cho trước hai số nguyên dương lẻ phân biệt m,n. Xét bảng ô vuông kích thước mtimes n gồm m dòng và n cột. Mỗi ô vuông con của bảng được tô bởi đúng một trong hai màu là xanh hoặc đỏ. Một dòng của bảng gọi là dòng đỏ nếu trên dòng đó có số ô vuông con được tô đỏ nhiều hơn số ô vuông con được tô xanh, một cột của bảng gọi là cột xanh nếu trên cột đó có số ô vuông con được tô xanh nhiều hơn số ô vuông con được tô đỏ.
a) Có bao nhiêu cách tô màu cho bảng sao cho mọi dòng đều là dòng đỏ?
b) Gọi...
Đọc tiếp
Cho trước hai số nguyên dương lẻ phân biệt m,n. Xét bảng ô vuông kích thước \(m\times n\) gồm m dòng và n cột. Mỗi ô vuông con của bảng được tô bởi đúng một trong hai màu là xanh hoặc đỏ. Một dòng của bảng gọi là dòng đỏ nếu trên dòng đó có số ô vuông con được tô đỏ nhiều hơn số ô vuông con được tô xanh, một cột của bảng gọi là cột xanh nếu trên cột đó có số ô vuông con được tô xanh nhiều hơn số ô vuông con được tô đỏ.
a) Có bao nhiêu cách tô màu cho bảng sao cho mọi dòng đều là dòng đỏ?
b) Gọi T là tổng của số dòng đỏ và số cột xanh trên bảng. Tìm giá trị lớn nhất của T.
(Câu a mình làm được rồi, các bạn giúp mình câu b với. Mình cảm ơn trước.)
1) Cho một bảng cỡ 2times n như hình vẽ.
Biết rằng mỗi ô có 1 số thực dương sao cho tổng 2 số trong mỗi cột đều bằng 1. CMR có thể chọn từ mỗi cột 1 số sao cho tổng các số được chọn trong mỗi hàng đều không quá dfrac{n+1}{4}
2) Trên bàn có 2004 cái hộp, mỗi hộp chứa 1 quả bóng. Biết rằng có một số chẵn (không nhỏ hơn 2) bóng màu trắng. Mỗi lần ta được phép chọn 2 hộp bất kì và hỏi xem liệu có ít nhất 1 quả bóng trắn...
Đọc tiếp
1) Cho một bảng cỡ \(2\times n\) như hình vẽ.
Biết rằng mỗi ô có 1 số thực dương sao cho tổng 2 số trong mỗi cột đều bằng 1. CMR có thể chọn từ mỗi cột 1 số sao cho tổng các số được chọn trong mỗi hàng đều không quá \(\dfrac{n+1}{4}\)
2) Trên bàn có 2004 cái hộp, mỗi hộp chứa 1 quả bóng. Biết rằng có một số chẵn (không nhỏ hơn 2) bóng màu trắng. Mỗi lần ta được phép chọn 2 hộp bất kì và hỏi xem liệu có ít nhất 1 quả bóng trắng trong 2 hộp đó hay không. Liệu cần hỏi ít nhất bao nhiêu lần để có thể xác định chắc chắn 1 hộp bất kì chứa bóng trắng?
Hai người cùng chơi trò chơi phóng phi tiêu, mỗi người đứng cách một tấm bảng hình vuông ABCD có kích thước là 4x4 dm một khoảng cách nhất định. Mỗi người sẽ phóng một cây phi tiêu vào tấm bảng hình vuông ABCD (như hình vẽ). Nếu phi tiêu cắm vào hình tròn tô màu hồng thì người đó sẽ được 10 điểm. Xét phép thử là hai người lần lượt phóng 1 cây phi tiêu vào tấm bảng hình vuông ABCD (phép thử này đảm bảo khi phóng là trúng và dính vào tấm bảng hình vuông, không rơi ra ngoài). Tính xác suất để c...
Đọc tiếp
Hai người cùng chơi trò chơi phóng phi tiêu, mỗi người đứng cách một tấm bảng hình vuông ABCD có kích thước là 4x4 dm một khoảng cách nhất định. Mỗi người sẽ phóng một cây phi tiêu vào tấm bảng hình vuông ABCD (như hình vẽ). Nếu phi tiêu cắm vào hình tròn tô màu hồng thì người đó sẽ được 10 điểm. Xét phép thử là hai người lần lượt phóng 1 cây phi tiêu vào tấm bảng hình vuông ABCD (phép thử này đảm bảo khi phóng là trúng và dính vào tấm bảng hình vuông, không rơi ra ngoài). Tính xác suất để có đúng một trong hai người phóng phi tiêu được 10 điểm. ( kết quả cuối cùng làm tròn số đến 4 chữ số thập phân)
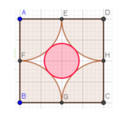
A. 0,2331
B. 0,2330
C. 0,2333
D. 0,2332
1) Cho một dãy vô hạn các ô như hình vẽ:
...
-2
-1
0
1
2
...
Ban đầu, ta có 2023 viên bi phân bố tùy ý trong các ô (mỗi ô có thể chứa nhiều viên bi). Mỗi bước ta chọn ra 2 viên bi ở 2 ô có số liên tiếp k và k+1 và chuyển chúng sang các ô k-1,k+2. CMR sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa.
2) Cho tam giác ABC nội tiếp (O), ngoại tiếp (I). Gọi D, E, F lần lượt la tiếp điểm của I với BC, CA, AB. Kẻ DKperp EFleft(Kin EFright). DKcapleft(Iright)...
Đọc tiếp
1) Cho một dãy vô hạn các ô như hình vẽ:
| ... | -2 | -1 | 0 | 1 | 2 | ... |
Ban đầu, ta có 2023 viên bi phân bố tùy ý trong các ô (mỗi ô có thể chứa nhiều viên bi). Mỗi bước ta chọn ra 2 viên bi ở 2 ô có số liên tiếp \(k\) và \(k+1\) và chuyển chúng sang các ô \(k-1,k+2\). CMR sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa.
2) Cho tam giác ABC nội tiếp (O), ngoại tiếp (I). Gọi D, E, F lần lượt la tiếp điểm của I với BC, CA, AB. Kẻ \(DK\perp EF\left(K\in EF\right)\). \(DK\cap\left(I\right)=G\left(\ne D\right)\). Gọi M là trung điểm BC. \(AG\cap\left(I\right)=H\), \(EF\cap\left(O\right)\) tại P và Q. CMR P, Q, D, H đồng viên.