Đáp án B
Do hệ phương trình đã cho có nghiệm là (1; 1) nên:
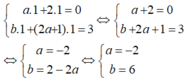
Vậy a = -2; b = 6
Đáp án B
Do hệ phương trình đã cho có nghiệm là (1; 1) nên:
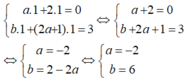
Vậy a = -2; b = 6
a) Xác định các hệ số a và b, biết rằng hệ phương trình 2 x + b y = − 4 b x − a y = − 5 có nghiệm (1 ; -2).
b) Cũng hỏi như vậy nếu phương trình có nghiệm là (√2 - 1; √2)
bài 1: giải các phương trình sau :
a) x^3-5x=0 b) căn bậc 2 của x-1=3
bài 2 :
cho hệ phương trình : {2x+my;3x-y=0 (I)
a) giải hệ phương trình khi m=0
b) tìm giá trị của m để hệ (I) có nghiệm (x;y) thỏa mãn hệ thức :
x-y+m+1/m-2=-4
bài 3:giải các phương trình sau
a)5x-2/3=5x-3/2 b) 10x+3/12=1+6x+8/9 c) 2(x+3/5)=5-(13/5+x) d) 7/8x-5(x-9)=20x+1,5/6
bài 1: Trong buổi lao động, 15 học sinh nam và nữ đã trồng được tất cả 180 cây. Biết rằng số cây các bạn nam trồng được số cây các bạn nữ trồng và mỗi bạn nam trồng nhiều hơn mỗi bạn nữ là 5 cây. Tính số bạn nam và nữ
bài 2:
1. Cho hệ phương trình \(\hept{\begin{cases}ax-y=2\\x+ay=3\end{cases}}\)
a) tìm a để hệ phương trình có nghiệm duy nhất và tìm nghiệm đó
b) tìm a để hệ phương trình vô nghiệm
2. cho hệ phương trình \(\hept{\begin{cases}ax-2y=a\\-2x+y=a+1\end{cases}}\)
a) tìm a để hệ phương trình có nghiệm duy nhất, khi đó tính x;y theo a
b) tìm a để hệ phương trình có nghiệm duy nhất thỏa mãn: x-y=1
c) tìm a để hệ phương trình có nghiệm duy nhất thỏa mãn x và y là các số nguyên
bài 3:
1.Chứng minh với mọi giá trị của m thì hệ phương trình \(\hept{\begin{cases}\left(m-1\right)x+y=2\\mx+y=m+1\end{cases}}\)(m là tham số) luôn có nghiệm duy nhất (x;y) thỏa mãn: \(2x+y\le3\)
2. Xác định giá trị của m để hệ phương trình \(\hept{\begin{cases}mx+5y=3\\x-3y=5\end{cases}}\)vô nghiệm
Bài 1: Cho hệ phương trình: \(\hept{\begin{cases}x+y=2a-1\\x^2+y^2=a^2+2a-3\end{cases}}\)
Giả sử (x; y) là nghiệm của hệ phương trình. Xác định a để xy đạt GTNN. Tìm GTNN đó.
Bài 2: Giải hệ phương trình: \(\hept{\begin{cases}\left(c+a\right)y+\left(a+b\right)z-\left(b+c\right)x=2a^3\\\left(a+b\right)z+\left(b+c\right)x-\left(c+a\right)y=2b^3\\\left(b+c\right)x+\left(c+a\right)y-\left(a+b\right)z=2c^3\end{cases}}\)
a)Định m và n để hệ phương trình sau có nghiệm là (2;1)
2mx-(n+1)y=m-n
(m+2)x+3ny=2m-3
b)Định a và b biết phương trình:ax2-2bx+3=0 có nghiệm là x=1 và x=-2
a) Giải hệ phương trình: \(\left\{{}\begin{matrix}\frac{2}{x}+y=3\\\frac{1}{x}-2y=4\end{matrix}\right.\)
b) Cho parabol (P): \(y=-\frac{1}{6}x^2\). Tìm tọa độ các điểm thuộc Parabol có tung độ y=-9.
c) Cho \(a=\sqrt{11+6\sqrt{2}},b=\sqrt{11-6\sqrt{2}}\). Chứng minh rằng a, b là hai nghiệm của một phương trình bậc hai với hệ số là số nguyên.
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Cho hệ phương trình
(a+1)x - y=3
ax-y=a
a)Giải hệ phương trình khi a = - căn 2
b) Xác định giá trị của a để hệ có nghiệm duy nhất thỏa mãn điều kiện x+y>0
Nếu có thể giải chi tiết giúp mình nhé
Cho hệ phương trình: a2x + y = 1 và x + y = a
a, giải hệ phương trình với a = -2
b, tìm các giá trị của a để hệ phương trình có vô số nghiệm
c, tìm a để hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x,y đều nguyên
1. Cho hệ PT : x - y =m ; mx + y = 1
a, Chứng tỏ hệ PT luôn có nghiệm
b, Tìm giá trị của m để hệ PT có nghiệm là một điểm thuộc góc phần tư thứ I
2. Viết PT đường thẳng (d) : y = ax + b biết (d) đi qua 2 điểm A và B :
a, A(3;2) và B(-1;-6)
b, A(3;0) và B(0;-6)