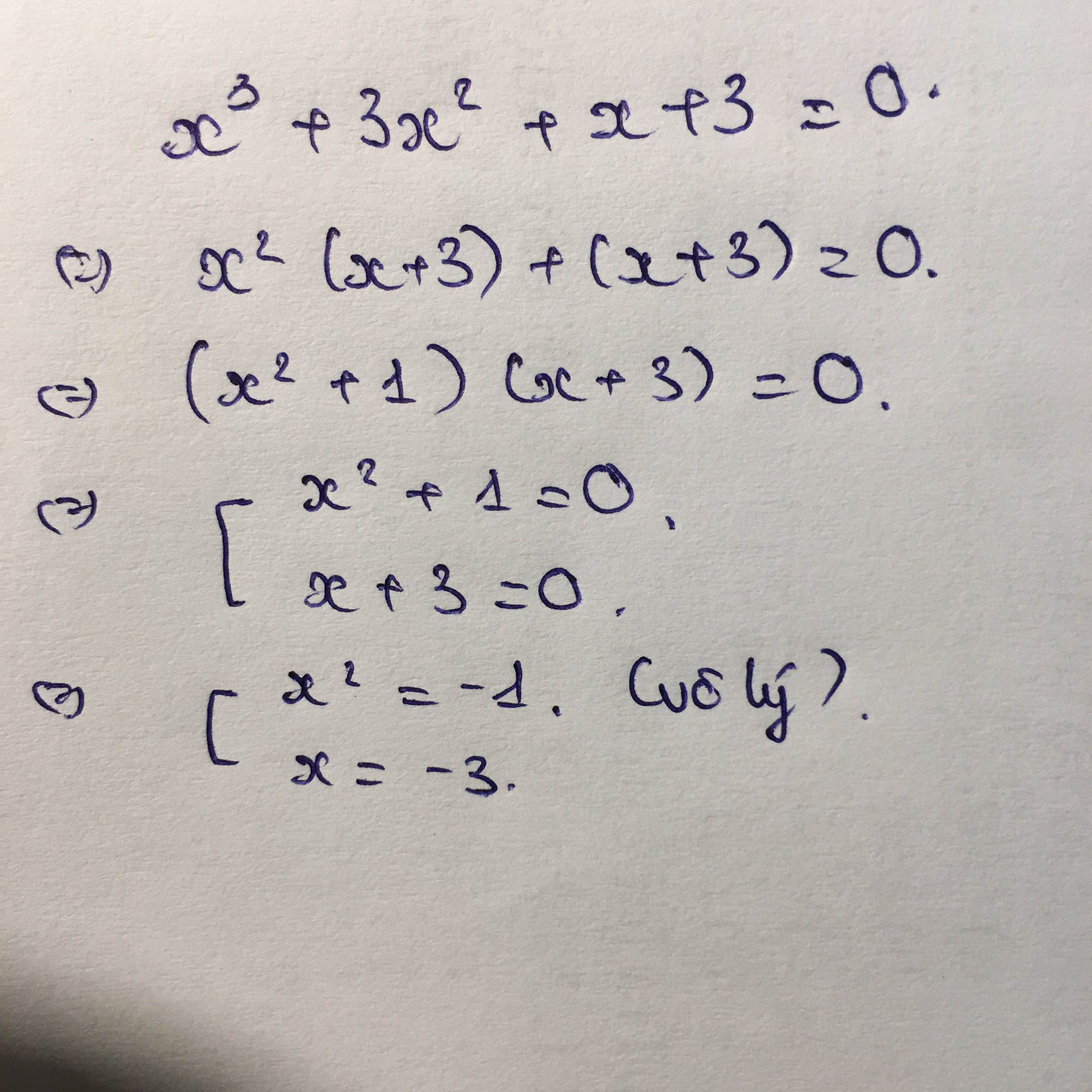Các câu hỏi tương tự
giải pt
a, 2x^3++3x^2-8x-12=0
b, x^3-4x^2-x+4=0
c,x^3-x^2-x-2=0
d,x^4-3x^3+3x^2-x=0
e,(x+1)(x^2-2x+3)=x^3+1
g,x^3+3x^2+3x+1=4x+4
Giải pT
1) x^3-5x^2+3x+1=0
2) x^4-3x^3+4x^2-3x+1=0
3) 3x^3+2x^2-4x-1=0
4) x^4+x^3-13x^2-x+10=0
5) x^4-2x^3-13x^2+14x+24=0
6) 3x^3+x^2-5x-3=0
Bài 4 : Tìm x biết
a)x( x-2 ) + x - 2 = 0
a) 5x( x-3 ) - x+3 = 0
b) (3x + 5)(4 – 3x) = 0
c) 3x(x – 7) – 2(x – 7) = 0
Giải các phương trình sau:
a \(x^2+3x+4=0\)
b \(3x^3-x+2=0\)
c \(x^4-4x^3-9x^2+8x+4=0\)
d \(x^4+4x^3+6x^2-5x-8=0\)
Đạo hàm y 0 −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 0, ∀x ∈ (0; 3) ⇔ m 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) 6x − 6; f 0 (x) 0 ⇔ x 1. Khi đó f(0) 1, f(3) 10, f(1) −2, suy ra max [0;3] f(x) f(3) 10. Do đó (∗) ⇔ m max [0;3] f(x) ⇔ m 10. Vậy với m 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Đọc tiếp
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
√3x+1=2x
√3x^2-10x-44=8-x
√x+3 + √3x+1 =4
(x+3)+(x-√4-x^2)=0
Xem chi tiết
Giải phương trình, x>0
\(\frac{\left(x^3+3x^2\sqrt{x^3-3x+6}\right)\left(3x-x^3-2\right)}{2+\sqrt{x^3-3x+6}}=4\left[2\sqrt{\left(x^3-3x+6\right)^3}-\left(x^3-3x+6\right)^2\right]\)
Giải phương trình, x>0
\(\frac{\left(x^3+3x^2\sqrt{x^3-3x+6}\right)\left(3x-x^3-2\right)}{2+\sqrt{x^3-3x+6}}=4\left[2\sqrt{\left(x^3-3x+6\right)^3}-\left(x^3-3x+6\right)^2\right]\)
x mũ 2 -(1+ căn 2 ) x + căn 2 =0
3x mũ 2 - căn 3x + căn 3 -3=0
x mũ 2 + căn 5x -11=0
ca8n3x mũ 2 -(1- căn 3)x -1=0
giải phương trình sau:
a) \(4x^2+\left(8x-4\right).\sqrt{x}-1=3x+2\sqrt{2x^2+5x-3}\)
b) \(8x^3-36x^2+\left(1-3x\right)\sqrt{3x-2}-3\sqrt{3x-2}+63x-32=0\)
c) \(2\sqrt[3]{3x-2}-3\sqrt{6-5x}+16=0\)
d) \(\sqrt[3]{x+6}-2\sqrt{x-1}=4-x^2\)