+ đường thẳng ∆1 có VTCP
+ đường thẳng ∆2 có VTCP
Để hai đường thẳng vuông góc thì
Nên: -3( m2+ 1) +(-m) .(-4m) = 0 =>m2-3= 0=>
Chọn A.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ? ∆1 : mx+ y-19 0 và ∆2 : (m-1) x+ (m+1) y-20 0 A. Mọi m. B.m 1 C. Không có m. D. m -1
Đọc tiếp
Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ?
∆1 : mx+ y-19 = 0 và ∆2 : (m-1) x+ (m+1) y-20 = 0
A. Mọi m.
B.m= 1
C. Không có m.
D. m= -1
Với giá trị nào của m hai đường thẳng sau đây song song ?
∆
1
:
x
8
+
(
m
+
1
)
t
y
10...
Đọc tiếp
Với giá trị nào của m hai đường thẳng sau đây song song ?
∆ 1 : x = 8 + ( m + 1 ) t y = 10 - t
và ∆2: mx + 6y – 76 = 0.
A. m = -3
B. m = 2
C. m = 3
D. Không có m thỏa mãn.
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10 0 và
d
2
:
x
2
-
3
t
y
1
-
4
m
t...
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 0 và
d
2
:
x
1
+
2
t
y
7
-
m
t
v...
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 = 0 và d 2 : x = 1 + 2 t y = 7 - m t vuông góc với nhau?
A. m = 3 2
B. m = 3
C. m = -3
D. m = - 3 2
Tìm tất cả các giá trị của a để hai đường thẳng sau vuông góc:
d
1
: x 1 - t, y 1 + 2t, z 3 + at,
d
2
: x a + at, y -1 + t, z -2 + 2t A. a-2 B. a2 C. a ≠ 2 D. Không tồn tại a
Đọc tiếp
Tìm tất cả các giá trị của a để hai đường thẳng sau vuông góc:
d 1 : x = 1 - t, y = 1 + 2t, z = 3 + at, d 2 : x = a + at, y = -1 + t, z = -2 + 2t
A. a=-2
B. a=2
C. a ≠ 2
D. Không tồn tại a
Với giá trị nào của m thì hai đường thẳng (∆1) : 2x- 3y - m 0 và
(
∆
2
)
:
x
2
2
t
y
1
+
m...
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng (∆1) : 2x- 3y - m= 0 và ( ∆ 2 ) : x = 2 = 2 t y = 1 + m t trùng nhau?
A. Không có m
B.m= -2
C. m = 4/3
D.m= 1
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y (3m + 2)x -7m – 1 vuông góc với đường thẳng
(
∆
)
:
y
2
x
-
1
A. m 0. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y = (3m + 2)x -7m – 1 vuông góc với đường thẳng ( ∆ ) : y = 2 x - 1
A. m = 0.
B. 
C. 
D.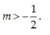 
Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = (3m + 2)x − 7m − 1 vuông góc với đường △ : y = 2x − 1.
A. m = 0
B. m = - 5 6
C. m < 5 6
D. m > - 1 2
7 tháng 7 2021 lúc 22:29
Trong phương vuông góc với Tọa độ Oxy, cho parabol (P): y = x² - 4mx + 3m² + 1, điểm A (0;3m) và đường thẳng (d): y = 2x + 3m-2 với m là tham số. Giả sử giao điểm của (d) và (P) là hai điểm M và N thì diện tích tam giác AMN bằng 4. Tìm giá trị của m