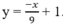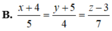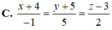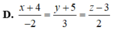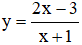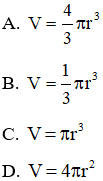Gọi M( x0; y0) , x 0 ≠ - 1 là tọa độ tiếp điểm của d và (C).
Khi đó d có hệ số góc y ' ( x 0 ) = 1 x 0 + 1 2 và có phương trình là :
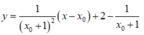
Vì d cách đều A: B nên d đi qua trung điểm I( -1; 1) của AB hoặc cùng phương với AB .
TH1: d đi qua trung điểm I( -1; 1) , thì ta luôn có:
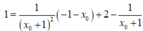 ,
,
phương trình này có nghiệm x0= 1
Với x0= 1 ta có phương trình tiếp tuyến d : 1 4 x + 5 4
TH2: d cùng phương với AB , tức là d và AB có cùng hệ số góc, khi đó
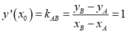
hay
1 x 0 + 1 2 = 1 ⇔ x 0 = - 2 h o ặ c x 0 = 0
Với x0 = -2 ta có phương trình tiếp tuyến d: y= x+ 5.
Với x0 =0 ta có phương trình tiếp tuyến d: y=x+ 1.
Vậy, có 3 tiếp tuyến thỏa mãn đề bài: y = 1 4 x + 5 4 , y= x+ 5, y=x+ 1
Chọn D.