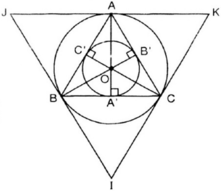
Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
Cho đường tròn (O;R). Viết công thức tính diện tích tam giác đều ngoại tiếp và diện tich tam giác đều nội tiếp (O;R). Áp dụng tính diện tích tam giác đều nội tiếp và tam giác đều ngoại tiếp khi R=1,123
Cho đường tròn (O; R) đường kính BC. Điểm A ở bên ngoài đường tròn với OA = 2R. Vẽ hai tiếp tuyến AD, AE với đường tròn (O; R) trong đó D, E là các tiếp điểm.
1. Chứng minh tứ giác ADOE nội tiếp và xác định tâm I của đường tròn ngoại tiếp tứ giác ADOE.
2. Chứng minh rằng tam giác ADE đều.
3. Vẽ DH vuông góc với CE với H thuộc CE . Gọi P là trung điểm của DH, CP cắt đường tròn (O) tại
điểm Q khác điểm C, AQ cắt đường tròn (O) tại điểm M khác điểm Q. Chứng minh: AQ . AM = 3R^2
4. Chứng minh đường thẳng AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ADQ.
Cho tam giác ABC đều có AB=6cm. Vẽ đường tròn nội tiếp, ngoại tiếp và bàng tiếp của tam giác ABC. Tính bán kính của đường tròn ngoại tiếp, nội tiếp và bàng tiếp
Cho tam giác ABC đều có AB=6cm. Vẽ đường tròn nội tiếp, ngoại tiếp và bàng tiếp của tam giác ABC. Tính bán kính của đường tròn ngoại tiếp, nội tiếp và bàng tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R).Qua tâm O vẽ các đường thẳng vuông góc với BC,AC lần lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N
1.chứng mình 4 điểm O,H,C,K cùng thuộc một đường tròn
2.chứng minh MN là trung trực của IC
3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC. Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC=120°
Cho tam giác ABC đều nội tiếp đường tròn (O;R). Vẽ đường tròn (I) tiếp xúc với AB, AC và tiép xúc trong với (O). Tính IB theo R
Cho tam giác ABC nội tiếp đường tròn (O;R).Quá tâm O vẽ các đường thẳng vuông góc với BC,AC lânf lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N;AM cắt BN tại I
1.chứng minh 4 điểmO,H,C,K cùng thuộc một đường tròn
2.chứng minh MN là trung trực của IC
3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC.Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC=120°