Các câu hỏi tương tự
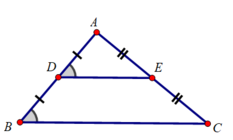
Bài 1:(5 điểm) : Xem hình vẽ sau:Giữa hai điểm B và C có chướng ngại vật. Để xác định được khoảng cách giữa hai điểm B và C ta chọn điểm A, rồi tìm vị trí hai điểm D và E theo thứ tự là trung điểm của AB và AC. Dùng thước đo DE ta sẽ xác định được khoảng cách giữa hai điểm B và C. Hỏi, nếu đo được DE 50m thì khoảng cách giữa hai điểm B và C là bao nhiêu? Vì sao?
Đọc tiếp
Bài 1:(5 điểm) : Xem hình vẽ sau:
Giữa hai điểm B và C có chướng ngại vật. Để xác định được khoảng cách giữa hai điểm B và C ta chọn điểm A, rồi tìm vị trí hai điểm D và E theo thứ tự là trung điểm của AB và AC. Dùng thước đo DE ta sẽ xác định được khoảng cách giữa hai điểm B và C. Hỏi, nếu đo được DE = 50m thì khoảng cách giữa hai điểm B và C là bao nhiêu? Vì sao?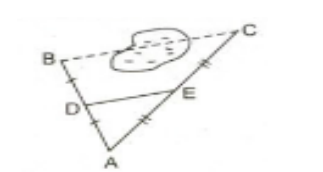
Cho tam giác ABC có AB < AC, điểm M bất kì thuộc cạnh BC . Qua M vẽ các đường thẳng vuông góc với AB tại I và AC tại J. Trên tia đối IM lấy D sao cho DI = IM. Trên tia đối JM lấy E sao cho J là trung điểm ME. Tìm vị trí của M để DE lớn nhất
Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
2. Cho tam giác ABC vuông tại A (ABAC), vẽ đường cao AH. Trên đoạn HC lấy điểm M (M không trùng với H,C) từ M vẽ MN vuông góc AC tại Na) C/M tam giác CMN đồng dạng với tam giác CAH và CA*CNCH*CMb) C/m tam giác ADE đồng dạng với tam giác ABC và góc ADE góc ABCc) Trên tia đối của tia AC lấy điểm D sao cho AD AC. Vẽ AE vuông góc BD tại E. Chứng minh góc BEH góc BCN. Gọi K,F lần lượt là trung điểm BH và BD. I là giao điểm của EK và CF. Chứng minh rằng KC*IE EF*IC
Đọc tiếp
2. Cho tam giác ABC vuông tại A (AB<AC), vẽ đường cao AH. Trên đoạn HC lấy điểm M (M không trùng với H,C) từ M vẽ MN vuông góc AC tại N
a) C/M tam giác CMN đồng dạng với tam giác CAH và CA*CN=CH*CM
b) C/m tam giác ADE đồng dạng với tam giác ABC và góc ADE= góc ABC
c) Trên tia đối của tia AC lấy điểm D sao cho AD < AC. Vẽ AE vuông góc BD tại E. Chứng minh góc BEH = góc BCN. Gọi K,F lần lượt là trung điểm BH và BD. I là giao điểm của EK và CF. Chứng minh rằng KC*IE = EF*IC
Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm và đường cao AH. Vẽ HD vuông góc AB tại D và HE vuông góc AC tại E. a) Vẽ tia vuông góc DE cắt BC tại M. Chứng minh M là trung điểm BC. b) Tính diện tích tam giác ADE
Cho tam giác ABC nhọn. M là điểm bất kì trên cạnh BC. D đối xứng với M qua AB, E đối xứng với M qua AC. DE cắt AB và AC lần lượt tại I và K.
a) Chứng minh tam giác ADE cân
b) Chứng minh MA là tia phân giác của góc IMK
c) Biết góc BAC bằng 70 độ .Tính các góc của tam giác ADE
1) Cho tam giác ABC có góc A tù. Trong góc A vẽ đoạn thẳng AD,AE sao cho AD vuông góc và bằng AB, AE vuông góc và bằng AC. Gọi M là trung điểm của DE. Chứng minh AM vuông góc với BC.
2) Cho tam giác đều ABC, một đường thẳng song song với BC cắt AB,AC ở D,E. Gọi G là trọng tâm của tam giác ADE, O là trung điểm CD. Tính góc GOB
Bài 1 :Cho ABC nhọn (AB AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.a/. Ch/m : ΔAMB ΔNMCb/. Vẽ CD bot AB (Din AB). So sánh góc ABC và góc BCN. Tính góc DCN.c/. Vẽ AH bot BC (H in BC), trên tia đối của tia HA lấy điểm I sao cho HI HA.Ch/m : BI CN.BÀI 2 :Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD AB; AE ACa) Chứng minh BE DCb) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC...
Đọc tiếp
Bài 1 :
Cho ABC nhọn (AB < AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.
a/. Ch/m : ΔAMB = ΔNMC
b/. Vẽ CD \bot AB (D\in AB). So sánh góc ABC và góc BCN. Tính góc DCN.
c/. Vẽ AH \bot BC (H \in BC), trên tia đối của tia HA lấy điểm I sao cho HI = HA.
Ch/m : BI = CN.
BÀI 2 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 3
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
BÀI 4
Cho tam giác ABC có góc A =350 . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
d) Tính góc ACB , biết góc BDH= 350 .
Bài 5 :
Cho tam giác ABC cân tại A và có \widehat{A}=50^0 .
Tính \widehat{B} và \widehat{C}
Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Chứng minh : DE // BC.
Bài 6 :
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
Chứng minh : DB = EC.
Gọi O là giao điểm của BD và EC. Chứng minh : tam giác OBC và ODE là tam giác cân.
Chứng minh rằng : DE // BC.
Bài 7
Cho tam giác ABC. Tia phân giác của góc C cắt AB tại D. trên tia đối của tia CA lấy điểm E sao cho CE = CB.
Chứng minh : CD // EB.
Tia phân giác của góc E cắt CD tại F. vẽ CK vuông góc EF tại K. chứng minh : CK Tia phân giác của góc ECF.
Bài 8 :
Cho tam giác ABC vuông tại A có \widehat{B}=60^0 . Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
Tam giác ACE đều.
A, E, F thẳng hàng.
Bài 4. Cho tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì (E khác A và D). Qua E kẻ các đường vuông góc với AB, AC lần lượt tại M và N. a) Chứng minh tứ giác AMEN là hình vuông. b) Chứng minh MN // BC. ...
Đọc tiếp
Bài 4. Cho tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì (E khác A và D). Qua E kẻ các đường vuông góc với AB, AC lần lượt tại M và N. a) Chứng minh tứ giác AMEN là hình vuông. b) Chứng minh MN // BC. c) Qua M kẻ đường thẳng vuông góc với DN tại F. Chứng minh AFE 90 độ d) Chứng minh B, E, F thẳng hàng.