Các câu hỏi tương tự
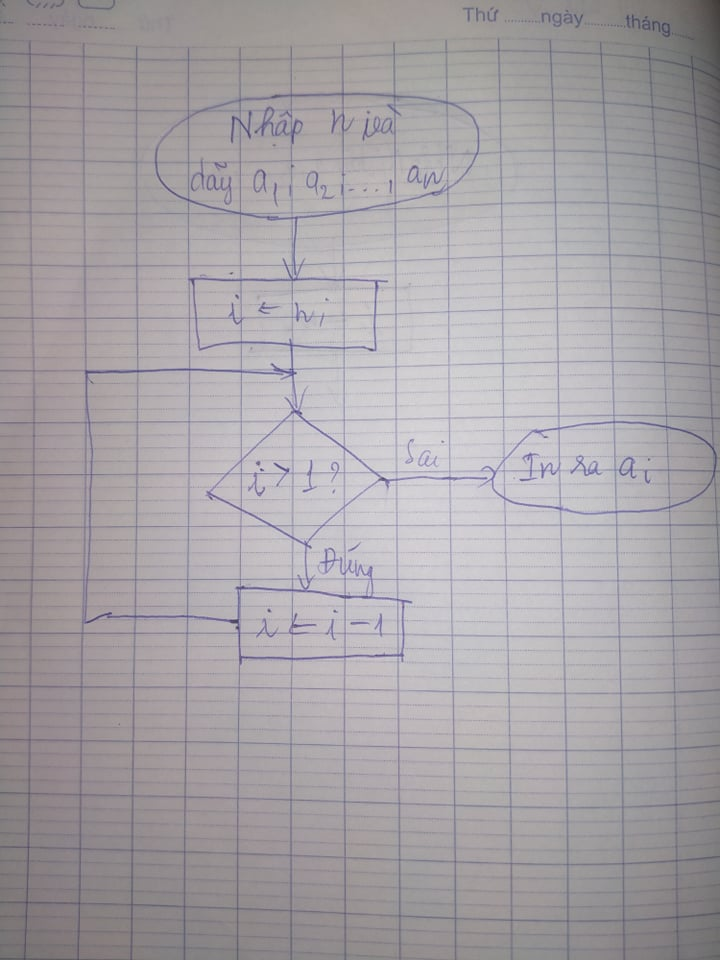
Vẽ sơ đồ khối biểu diễn thuật toán nhập dãy số a1,a2,a3,….,an , xuất ra màn hình 3 số âm lớn nhất trong dãy
Viết chương trình nhập từ bàn phím số nguyên dương N (N100) và dãy A gồm N số nguyên A1, A2, …AN. Tìm và in ra số nhỏ nhất của dãy số vừa nhập? Sắp xếp dãy số A theo thứ tự giảm dần và in ra màn hình. Input: Số nguyên dương N và dãy số A gồm N số nguyên dương a1, a2, …, an. Output: In ra Phần tử nhỏ nhất của dãy số đó. Sắp xếp dãy số A theo thứ tự giảm dần và in ra màn hình.
Đọc tiếp
Viết chương trình nhập từ bàn phím số nguyên dương N (N<=100) và dãy A gồm N số nguyên A1, A2, …AN. Tìm và in ra số nhỏ nhất của dãy số vừa nhập? Sắp xếp dãy số A theo thứ tự giảm dần và in ra màn hình. Input: Số nguyên dương N và dãy số A gồm N số nguyên dương a1, a2, …, an. Output: In ra Phần tử nhỏ nhất của dãy số đó. Sắp xếp dãy số A theo thứ tự giảm dần và in ra màn hình.
Bài 1 (8 điểm): TÍNH TỔNGCho dãy số a1, a2,..., aN và một số S. Hãy tính tổng các phần tử trong dãy mà chia hết cho SDữ liệu: Vào từ tệp văn bản BAI1.INP:Dòng 1 : Hai số nguyên dương N và S (N ⩽ 105, S ⩽ 109)Dòng 2 : N số nguyên dương a1, a2,..., aN (ai ⩽ 109)Kết quả: Ghi ra tệp văn bản BAI1.OUT kết quả tìm được.Ví dụ:BAI1.INPBAI1.OUT5 22 4 6 8 10 30
Đọc tiếp
Bài 1 (8 điểm): TÍNH TỔNG
Cho dãy số a1, a2,..., aN và một số S. Hãy tính tổng các phần tử trong dãy mà chia hết cho S
Dữ liệu: Vào từ tệp văn bản BAI1.INP:
Dòng 1 : Hai số nguyên dương N và S (N ⩽ 105, S ⩽ 109)
Dòng 2 : N số nguyên dương a1, a2,..., aN (ai ⩽ 109)
Kết quả: Ghi ra tệp văn bản BAI1.OUT kết quả tìm được.
Ví dụ:
BAI1.INP | BAI1.OUT |
5 2 2 4 6 8 10 | 30
|
Viết chương trình nhập vào một mảng gồm n phần tử nguyên, hiểnthị mảng đã nhập ra màn hình, thực hiện sắp xếp mảng vừa nhập theo thứ tự tăng dầnbằng thuật toán sắp xếp chèn (Insert_sort). Sử dụng thuật toán tìm kiếm nhị phân đểtìm một phần tử k bất kỳ trong mảng, với k nhập từ bàn phím, hiển thị vị trí của k nếutìm thấy, và -1 nếu không tìm thấy k. (Viết bằng ngôn ngữ C++)
Đọc tiếp
Viết chương trình nhập vào một mảng gồm n phần tử nguyên, hiển
thị mảng đã nhập ra màn hình, thực hiện sắp xếp mảng vừa nhập theo thứ tự tăng dần
bằng thuật toán sắp xếp chèn (Insert_sort). Sử dụng thuật toán tìm kiếm nhị phân để
tìm một phần tử k bất kỳ trong mảng, với k nhập từ bàn phím, hiển thị vị trí của k nếu
tìm thấy, và -1 nếu không tìm thấy k. (Viết bằng ngôn ngữ C++)
Viết chương trình nhập vào 1 dãy điểm x1y1, x2y2...xn,yn. In các điểm vừa nhập ra màn hình, tính tổng độ dài gấp khúc lần lượt đi qua các điểm thứ 1, 2,..n. Đếm số điểm thuộc góc phần tư thứ 2. Tìm khoảng các xa gốc tọa độ (trục hoành, trục tung) nhất.
Cho một dãy số A gồm N phần tử (n>=100)
Hãy phát sinh dãy A ngẫu nhiên N phần tử (10<=n<=N).Xuất dãy A ra màn hình
C++;Cho 1 dãy gồm n số nguyên A(a1,a2,...,an) và 1 số nguyên k. hãy xác định xem trong dãy A có tồn tại 2 phần tử a[p] và a[q] ở 2 vị trí khác nhau p khác q mà a[p] - a[q]k hay không.Input:-Dòng 1 chứa số nguyên n và k(2n10^5,|k|2.10^9)-Dòng 2 chứa n sô nguyên a1,a2,...,an (với mọi |a[i]2.10^9)Output: Ghi ra 2 chỉ sô p,q tìm đc. Nếu không tồn tại cặp số thỏa mãn yêu cầu, ghi ra 2 số 0.
Đọc tiếp
C++;
Cho 1 dãy gồm n số nguyên A=(a1,a2,...,an) và 1 số nguyên k. hãy xác định xem trong dãy A có tồn tại 2 phần tử a[p] và a[q] ở 2 vị trí khác nhau p khác q mà a[p] - a[q]=k hay không.
Input:
-Dòng 1 chứa số nguyên n và k(2<=n<=10^5,|k|<=2.10^9)
-Dòng 2 chứa n sô nguyên a1,a2,...,an (với mọi |a[i]<=2.10^9)
Output: Ghi ra 2 chỉ sô p,q tìm đc. Nếu không tồn tại cặp số thỏa mãn yêu cầu, ghi ra 2 số 0.
Viết giải thuật tính trung bình cộng của một dãy bất kỳ có n số và đánh giá độ phức tạp của thuật toán
NGÔN NGỮ C GIÚP MÌNH VỚI Ạ. 3.Viết chương trình tính tổng nghịch đảo của n số nguyên đầu tiên, theo công thức sau: S 1 + 1/2 + 1/3 + …+ 1/n 5.Viết chương trình nhập số nguyên dương n từ bàn phím, n10, tính và đưa ra màn hình giá trị n! 6.Viết chương trình tính và in tổng dưới đây ra màn hình: S 1 + 1/(2!) + 1/(3!) + .. + 1/(n!) với n được nhập từ bàn phím, 0n10. 8.Viết chương trình in ra các số nguyên tố từ 2 đến n, với n nhập từ bàn phím. 10.Nhập tử số và mẫu số của một phân số, in phân số đó...
Đọc tiếp
NGÔN NGỮ C GIÚP MÌNH VỚI Ạ. 3.Viết chương trình tính tổng nghịch đảo của n số nguyên đầu tiên, theo công thức sau: S = 1 + 1/2 + 1/3 + …+ 1/n 5.Viết chương trình nhập số nguyên dương n từ bàn phím, n<=10, tính và đưa ra màn hình giá trị n! 6.Viết chương trình tính và in tổng dưới đây ra màn hình: S = 1 + 1/(2!) + 1/(3!) + .. + 1/(n!) với n được nhập từ bàn phím, 0<n<10. 8.Viết chương trình in ra các số nguyên tố từ 2 đến n, với n nhập từ bàn phím. 10.Nhập tử số và mẫu số của một phân số, in phân số đó dưới dạng tối giản.