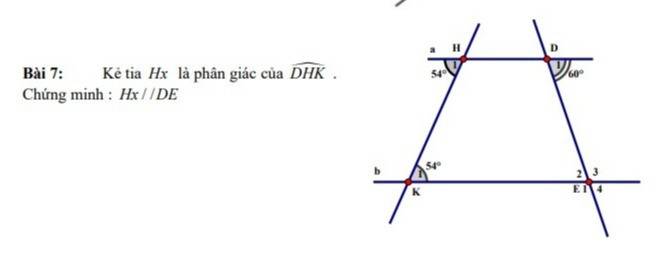
vẽ hình +giải
Bài 5. Cho tam giác \(ABC\) và \(M\) là một điểm nằm trong tam giác. Gọi \(I\) là giao điểm của đường thẳng \(BM\) với cạnh \(AC\).
a) So sánh \(MA\) với \(MI + IA\)
b) Chứng minh \(MA + MB < IB + IA\)
c) Chứng minh \(IB + IA < CA + CB\)
d) Chứng minh \(MA + MB < CA + CB\)
Bài 6. Cho góc nhọn \(xOy\), trên \(Ox\) lấy 2 điểm \(M, N\) (\(M\) nằm giữa \(O\) và \(N\)). Trên \(Oy\) lấy \(E\) và \(F\) (\(E\) nằm giữa \(O\) và \(F\)). Chứng minh rằng: \(MN + EF < MF + NE\).
Giải (vẽ hộ hình)
Vẽ góc BCA = 75 độ , vẽ đường thẳng x,y song song vớ AC tạo thành một hình tam giác ; vẽ BAE = 70 độ ( ko cần vẽ hình )
Tính x, y biết AE // BC
Ai giải nhanh và đúng mk sẽ tick
Giải theo ý hiểu của các bạn !!
Vẽ hình sau đó giải
Giải với vẽ hộ hình
Cho hình vẽ chứng minh rằng BD + CE <AB + AC giải giúp mình nha ! Vẽ hình giúp mình luôn nha
help me bắt buộc phải vẽ hình vẽ giải thích ngắn nhất có thể pls
Giải hộ vẽ cả hình nhé
giúp mik vẽ hình và giải lun
Ai giải vs vẽ hộ hình vs
