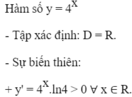
⇒ Hàm số đồng biến trên R.
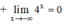
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
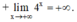
+ Bảng biến thiên:
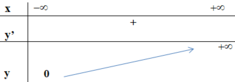
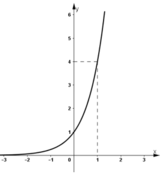
- Đồ thị:
+ Đồ thị hàm số đi qua (0; 1) và (1; 4).
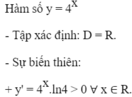
⇒ Hàm số đồng biến trên R.
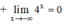
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
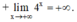
+ Bảng biến thiên:

- Đồ thị:
+ Đồ thị hàm số đi qua (0; 1) và (1; 4).

Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 3x – 2
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 2 – 3x
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 3x + 2
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = |3x – 2|
Cho đồ thị hàm số
y
=
1
2
(
x
-
1
)
(
x
2
-
4
)
như hình vẽ bên. Số điểm cực trị của đồ thị hàm số
f
(
x
)
=
x
-
1
(
x
2
-
4
)
+
m
, với m thuộc đoạn (2;6) là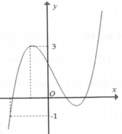
![]()
![]()
![]()
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
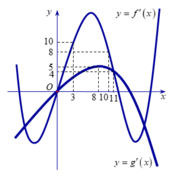
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Vẽ đồ thị của các hàm số y = x 2 và y = x 1 2 trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi x = 0,5; 1; 3/2; 2; 3; 4.
Vẽ đồ thị của các hàm số y =
x
2
và 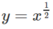 trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi x = 0,5; 1; 3/2; 2; 3; 4.
trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi x = 0,5; 1; 3/2; 2; 3; 4.
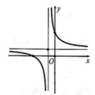
Hàm số y=f(x) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y=|f(x)|
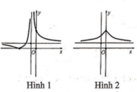
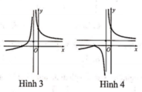
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
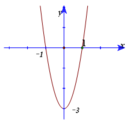
A. y =x3-3x+2.
B. y=x3+3x+2.
C. y=x3-2x+2.
D. y =x3-3x-1.