Vật sang AB được đặt song song với màn và cách màn một khoảng cố định a.Một thất kính hội tụ có trục chính qua điểm A và vuông góc với màn được di chuyển giữa vật và màn. Người ta nhận thấy có một vị trí của thấu kính tạo ảnh rõ nét của vật trên màn, ảnh lớn hơn vật. Hãy chứng tỏ rằng, còn một vị trí thứ hai của thấu kính ở trong khoảng cách giữa vật và màn tạo được ảnh rõ nét của vật trên màn.
Sơ đồ tạo ảnh:
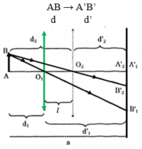
Ta có: 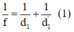
Theo giả thiết: vật thật và ảnh trên màn ⇒ ảnh thật lớn hơn vật suy ra:
a = d1 + d’1 và d’1 > d1 > f > 0 (2)
Từ (1) và (2) ta có: d1.d’1 = f.(d1 + d’1) = f.a (3)
Theo định lý Vi-et đảo thì d1 và d’1 là nghiệm của phương trình: X2 – a.X + f.a = 0 (4)
Điều kiện để có hai vị trí của thấu kính cho ảnh rõ nét trên màn (E) là phương trình (4) phải có hai nghiệm X1 và X2.
Do đó ta phải có: Δ = a2 - 4fa ≥ 0 ⇒ f < a/4
Theo bất đẳng thức Cô-si:
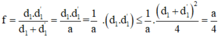
Vậy điều kiện Δ = a2 - 4fa ≥ 0 luôn đúng. Trường hợp Δ = 0 thì d1 = d’1 = a/2, khi đó 2 vị trí của thấu kính trùng nhau.
⇒ luôn tồn tại hai vị trí của thấu kính trong khoảng Vật-Màn đều cho ảnh rõ nét trên màn (ĐPCM)



