Đáp án : C
Để đi từ A đến C (qua B); ta cần thực hiện 2 bước sau:
Bước 1: Đi từ A đến B có 5 cách chọn con đường.
Bước 2: Đi từ B đến C có 5 cách chọn con đường.
Do đó theo quy tắc nhân có tổng cộng 5.5 = 25 cách chọn đường từ A đến C (qua B).
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án : C
Để đi từ A đến C (qua B); ta cần thực hiện 2 bước sau:
Bước 1: Đi từ A đến B có 5 cách chọn con đường.
Bước 2: Đi từ B đến C có 5 cách chọn con đường.
Do đó theo quy tắc nhân có tổng cộng 5.5 = 25 cách chọn đường từ A đến C (qua B).
Từ A đến B có 6 con đường, từ B đến C có 4 con đường. Hỏi có bao nhiêu cách chọn đường từ A đến C (qua B) và trở về C đến A (qua B) và không đi lại các con đường đã đi rồi?
A. 240
B. 132
C. 180
D. 150
Từ thành phố A đến thành phố B có ba con đường, từ B đến C có bốn con đường (h.25). Hỏi có bao nhiêu cách đi từ A đến C, qua B?
Từ thành phố A có 10 con đường đến thành phố B. Từ thành phố A có 9 con đường đến thành phố C. Từ thành phố B có 6 con đường đến thành phố D. Từ thành phố C có 11 con đường đến thành phố D. Không có con đường nào nối B với C. Hỏi có bao nhiêu cách đi từ A đến D?
A. 156
B. 157
C. 159
D. 176
Từ thành phố A đến thành phố B có 5 con đường. Từ thành phố B đến thành phố C có 3 con đường. Hỏi có bao nhiêu cách đi tử A đến C mà qua B một lần?
A. 8
B. 15
C. 3
D. 5
1.Có 5 con đường đi từ A đến B và 9 con đường đi từ B đến C. Hỏi có bao nhiêu cách đi từ A đến C mà chỉ qua B một lần?
A. 45 B.14 C.9 D.2
2. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.y=-sin x B. y=sin2x+ sin x C. y= tan x * sin x D.y= tan x + cos X
3. Phương trình sin x=\(\dfrac{1}{2}\) có bao nhiêu nghiệm trên ( 0;π) ?
A. 0 B.1 C. 2 D.3
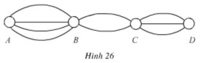
Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

A. 10
B. 9
C. 24
D. 18
Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

A. 9.
B. 10.
C. 18.
D. 24.
Dưới thành phố A, B, C, D được nối với nhau bởi các con đường như hình dưới:
Hỏi: Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
Giữa hai thành phố A và B có 5 con đường đi. Hỏi có bao nhiêu cách đi từ A đến B rồi trở về A mà không có đường nào được đi hai lần?