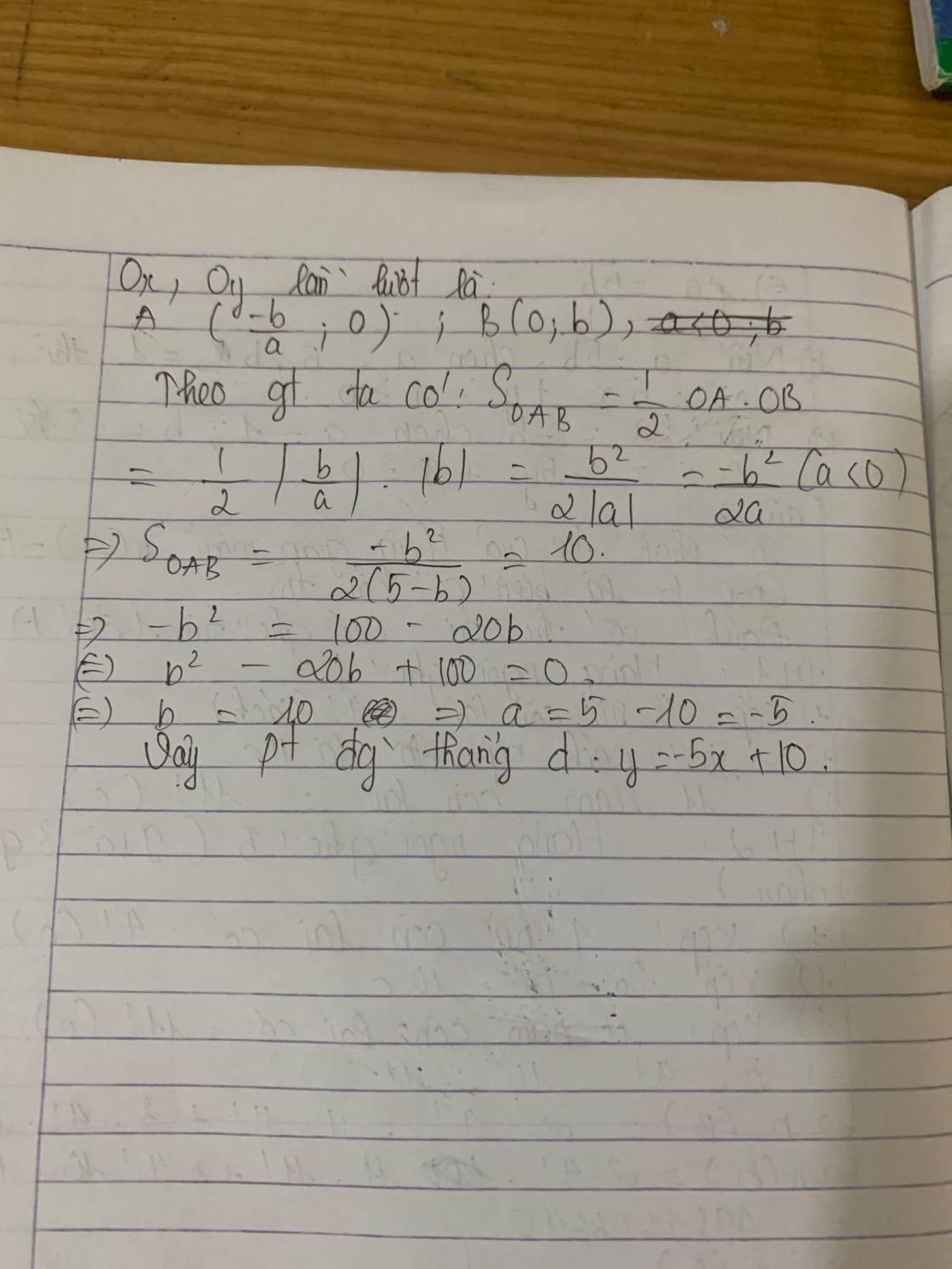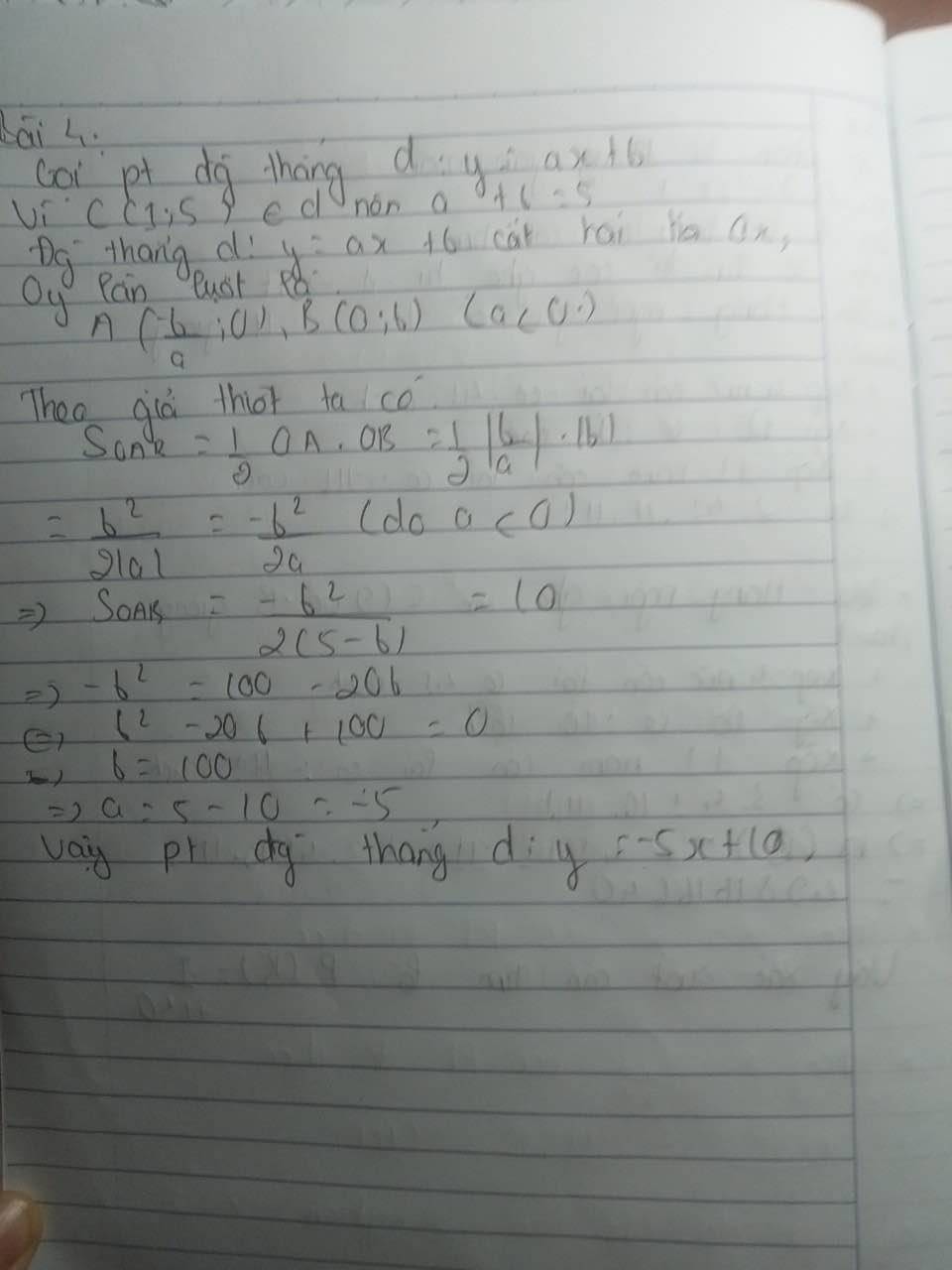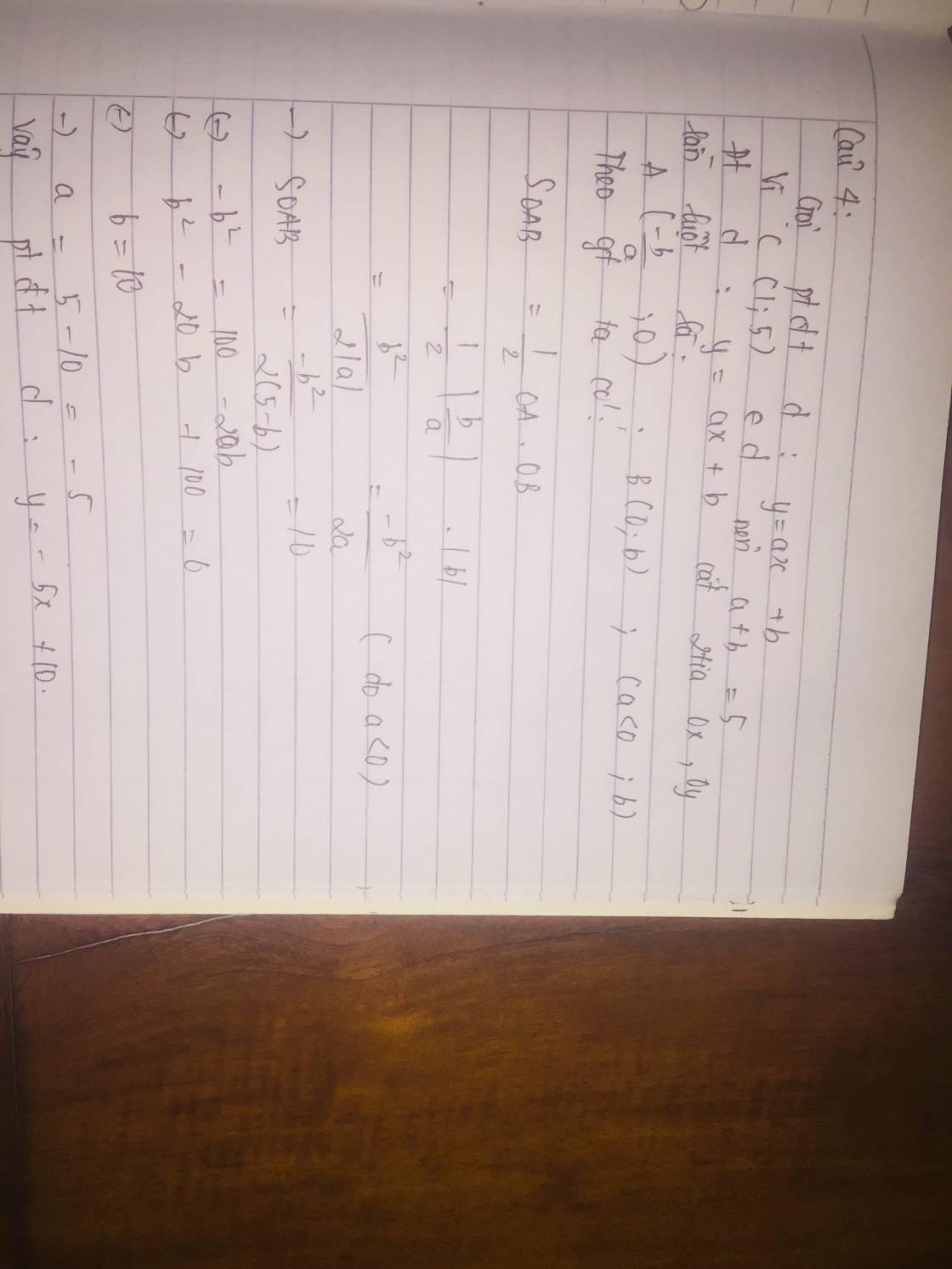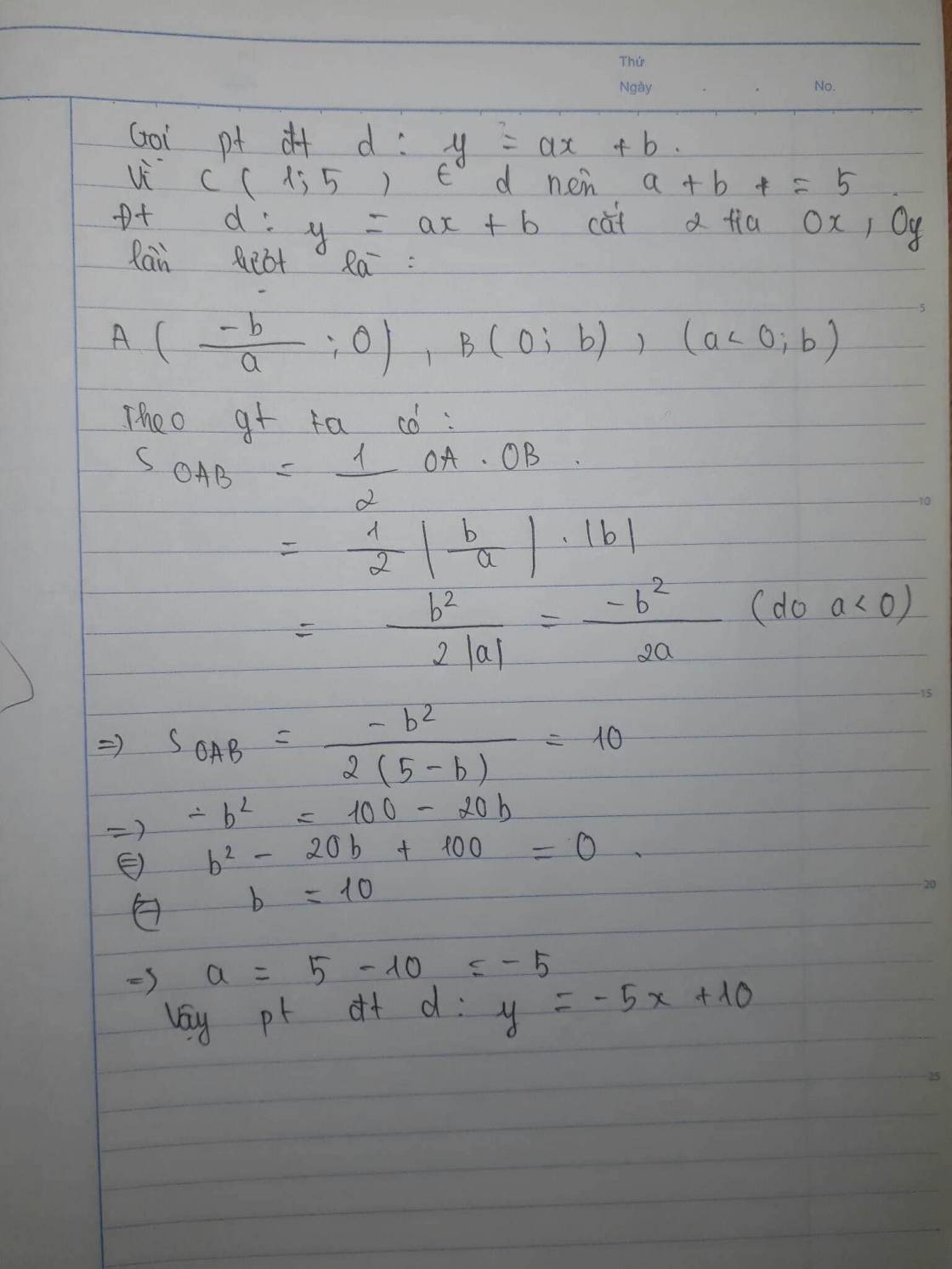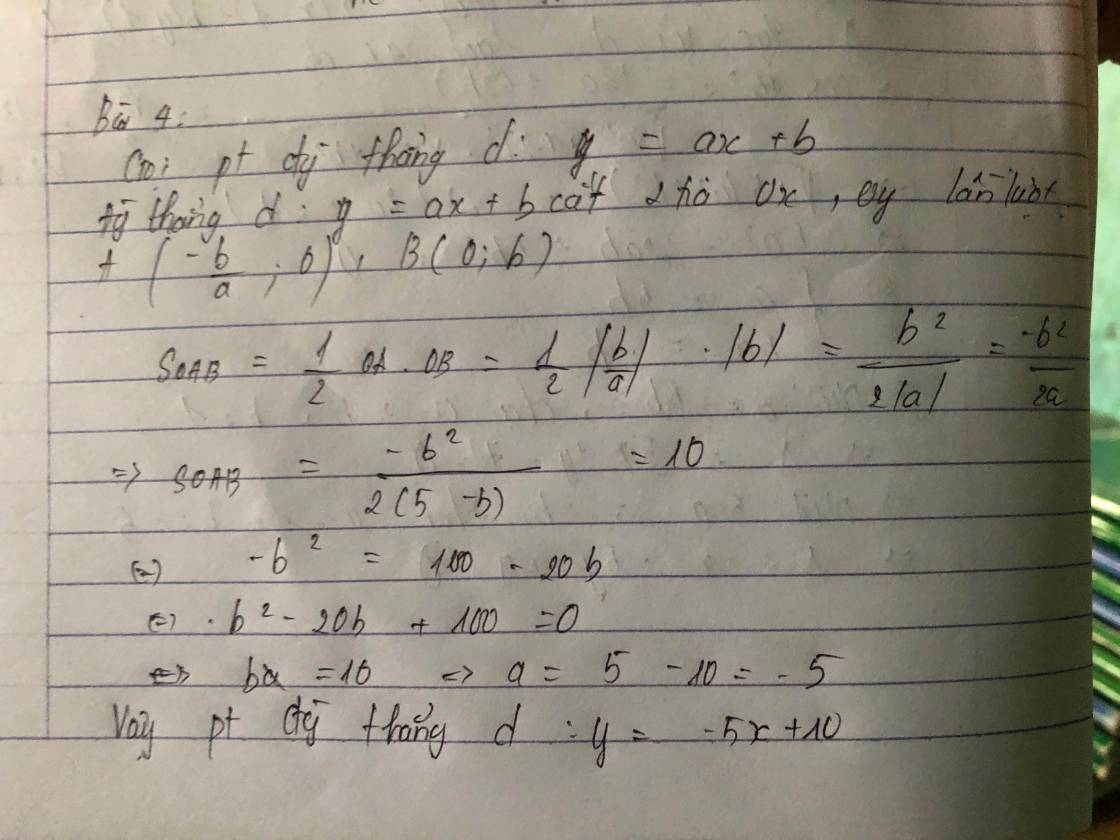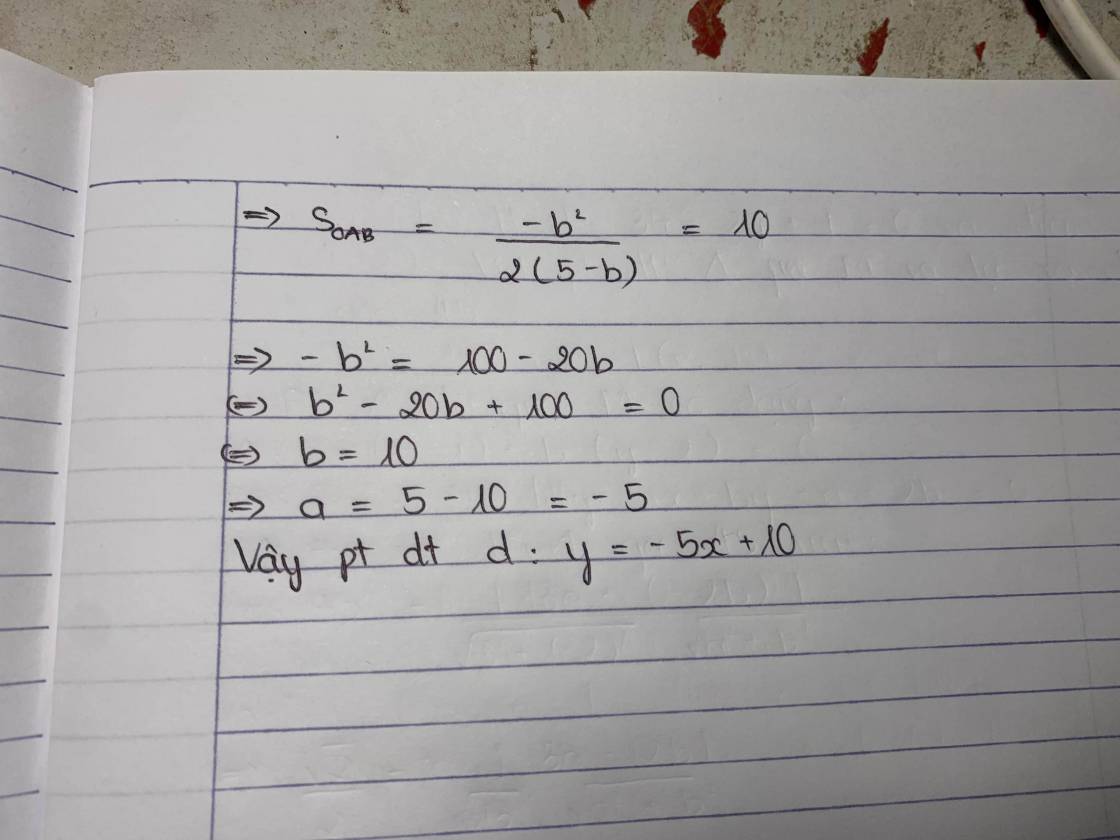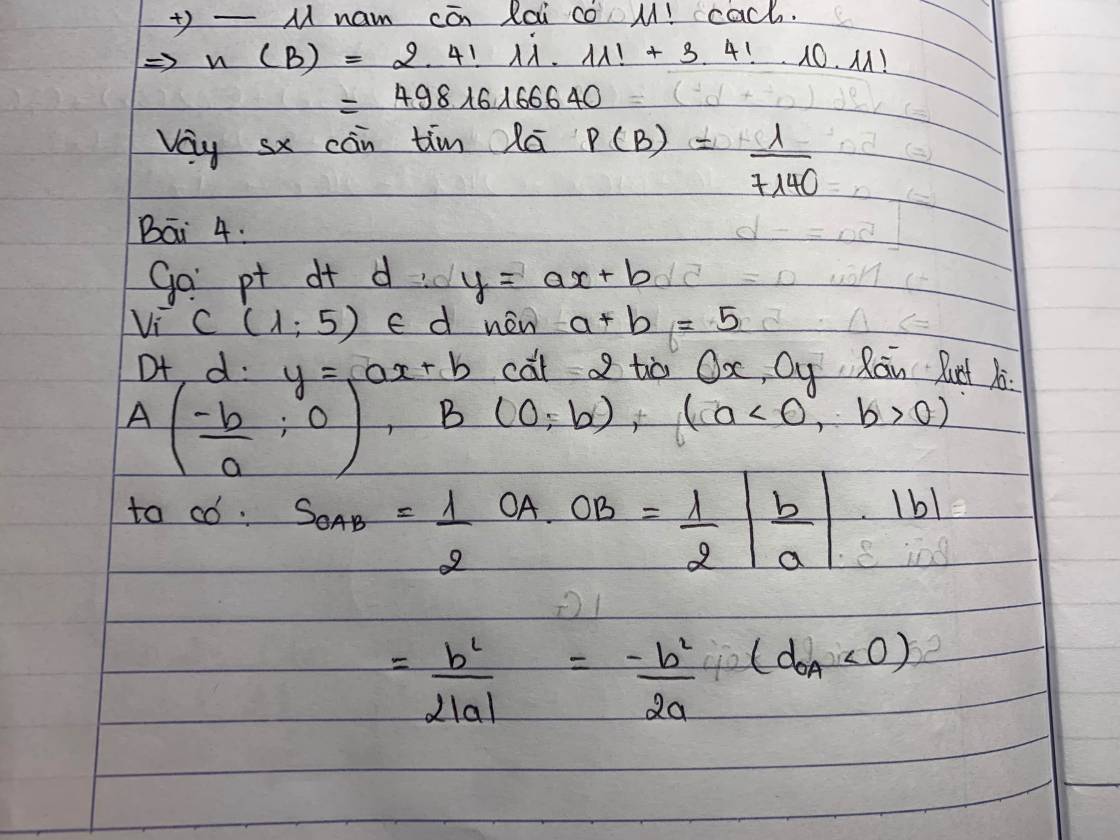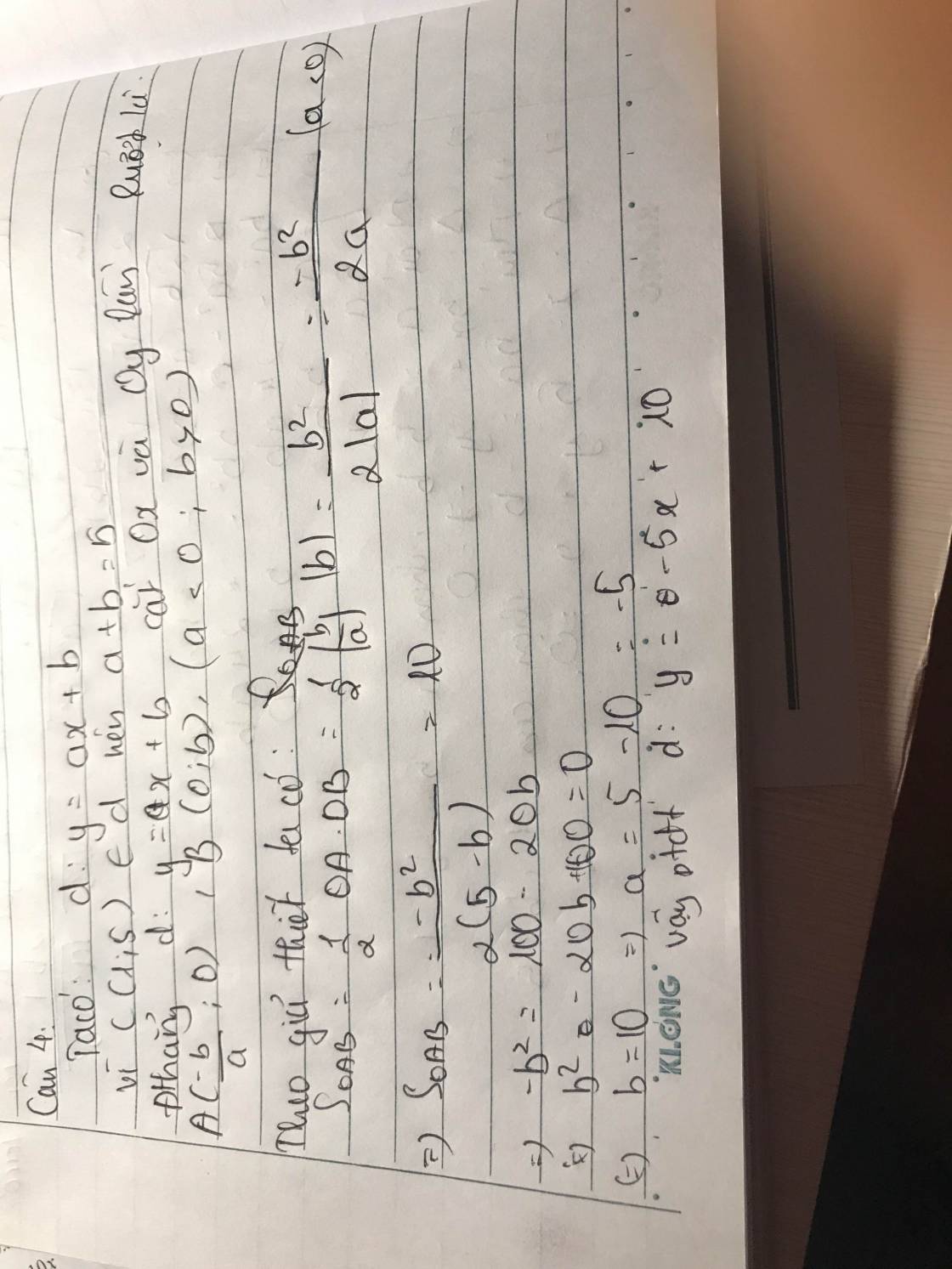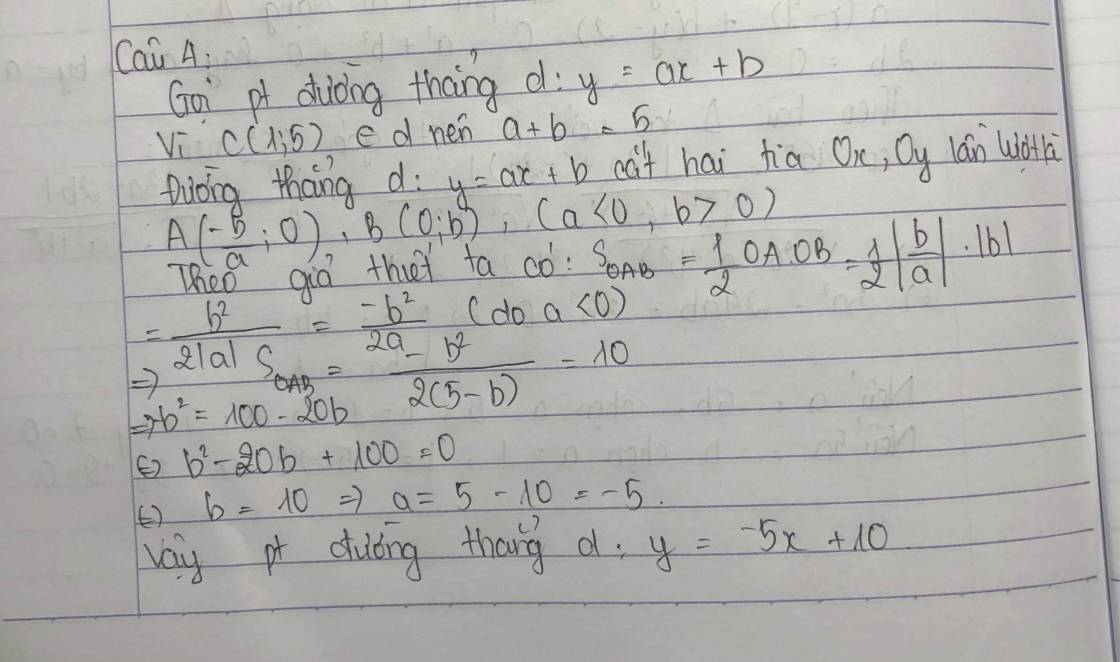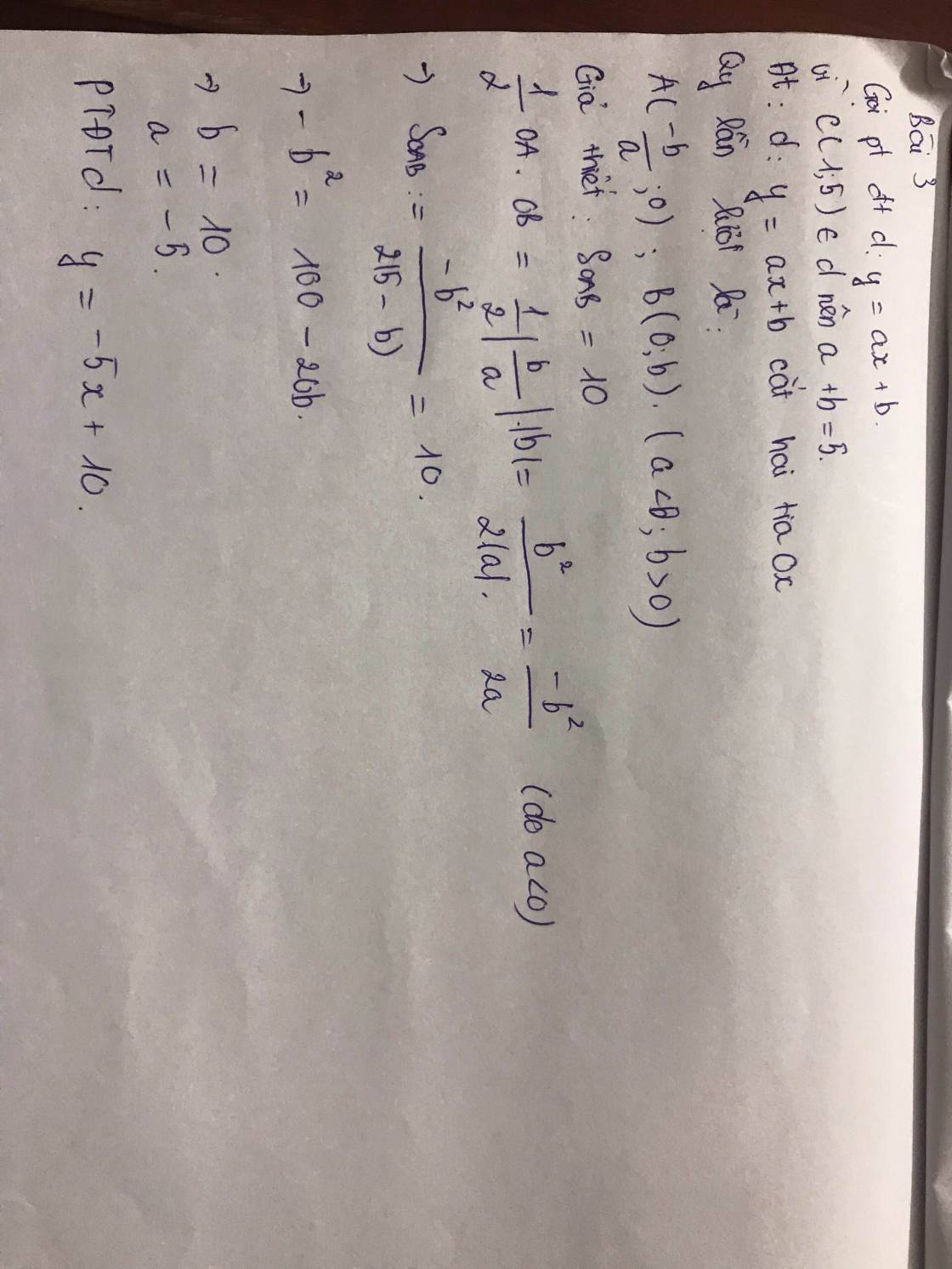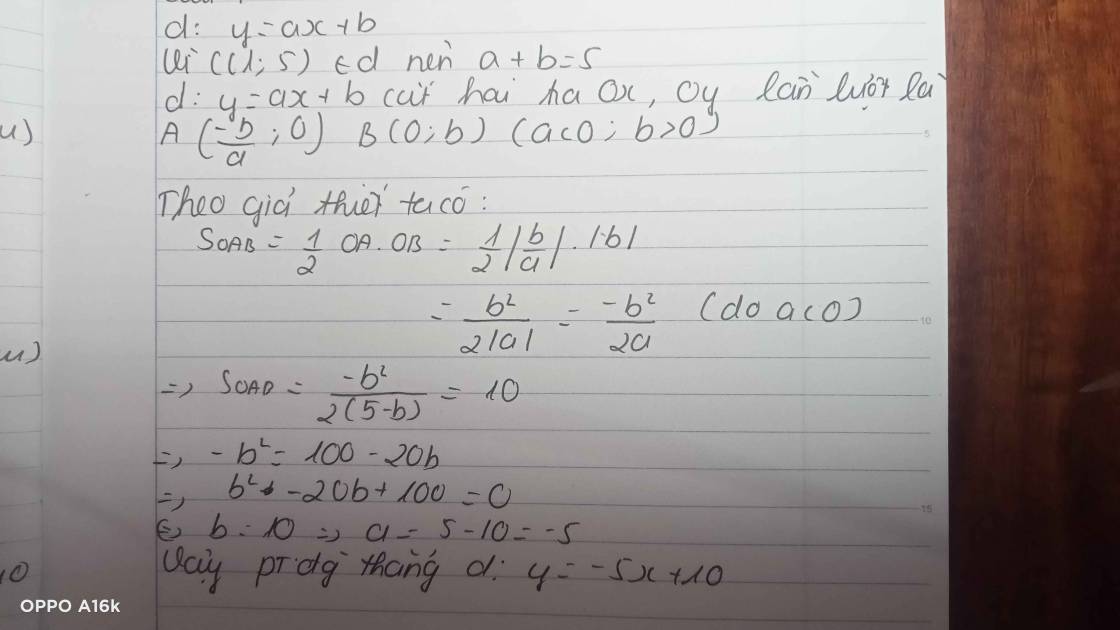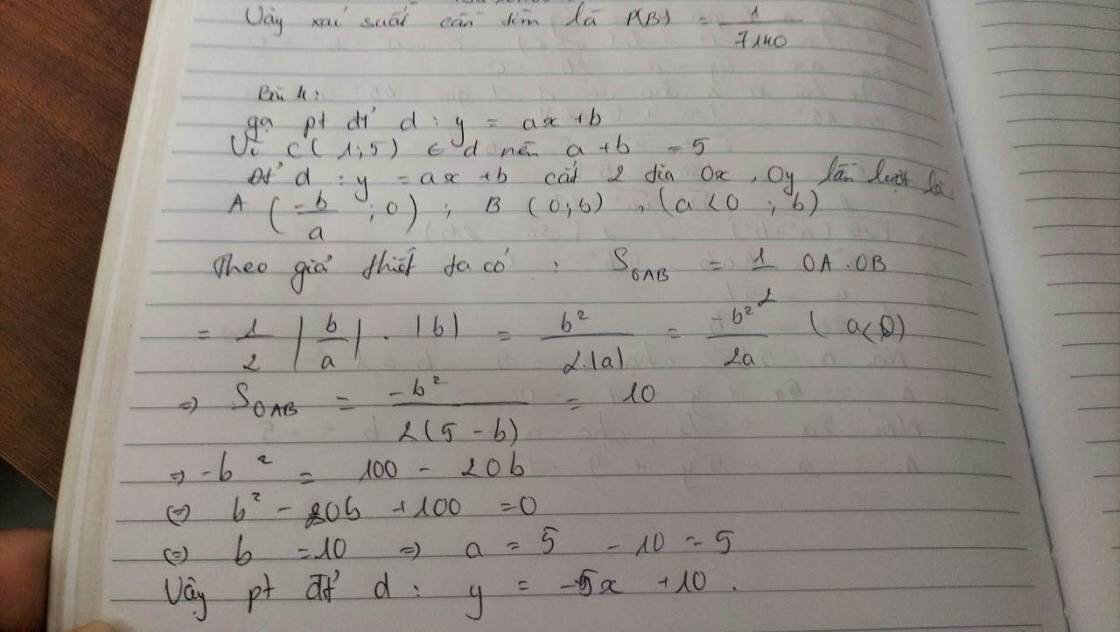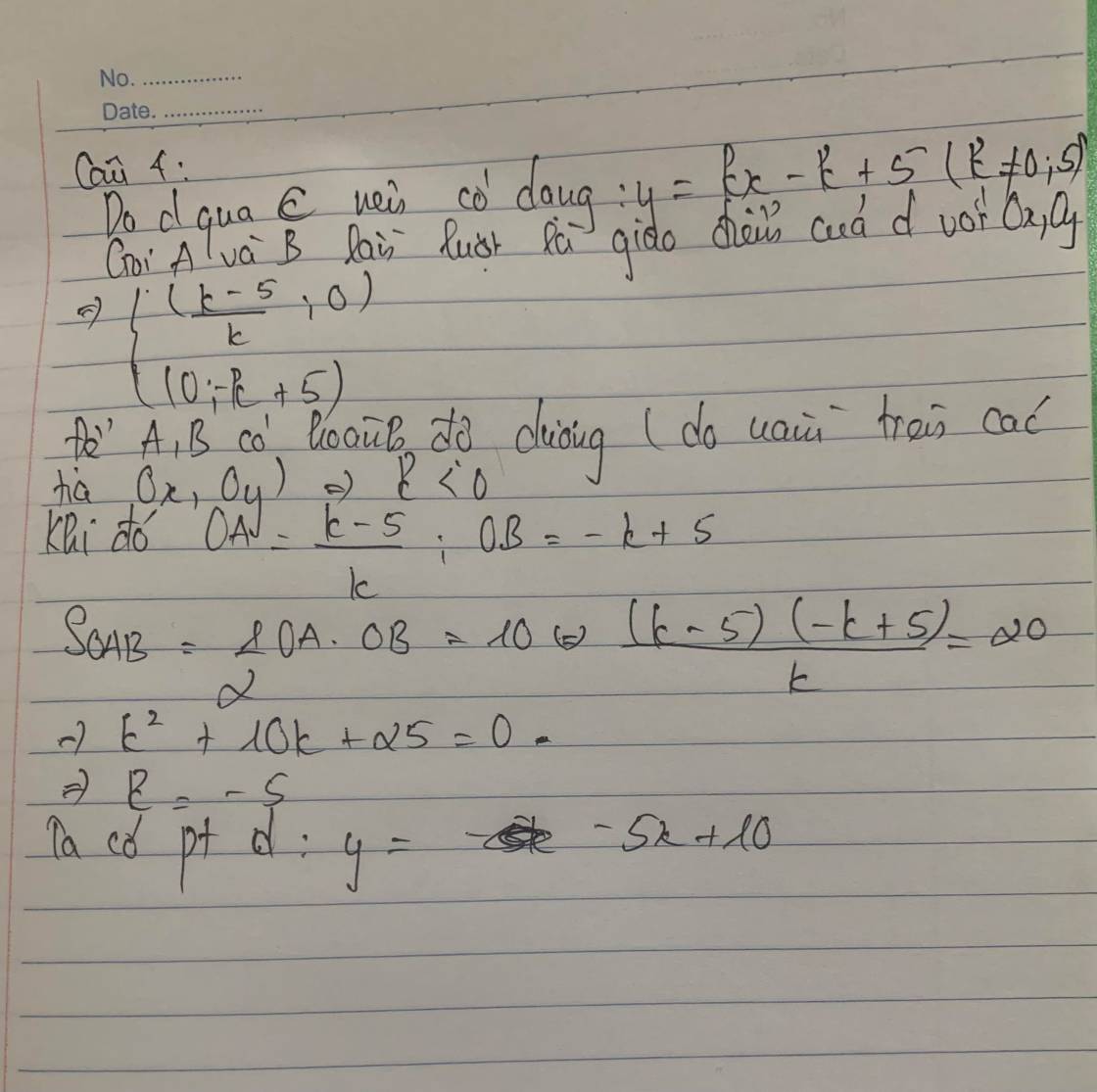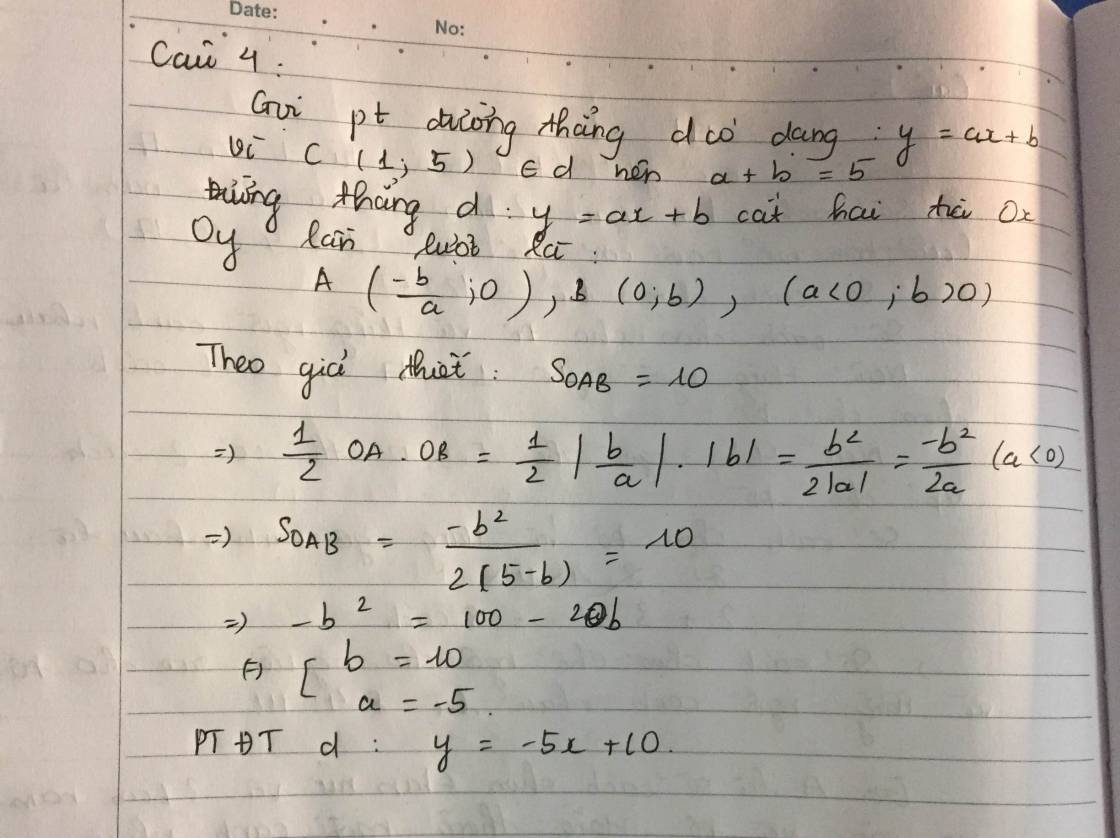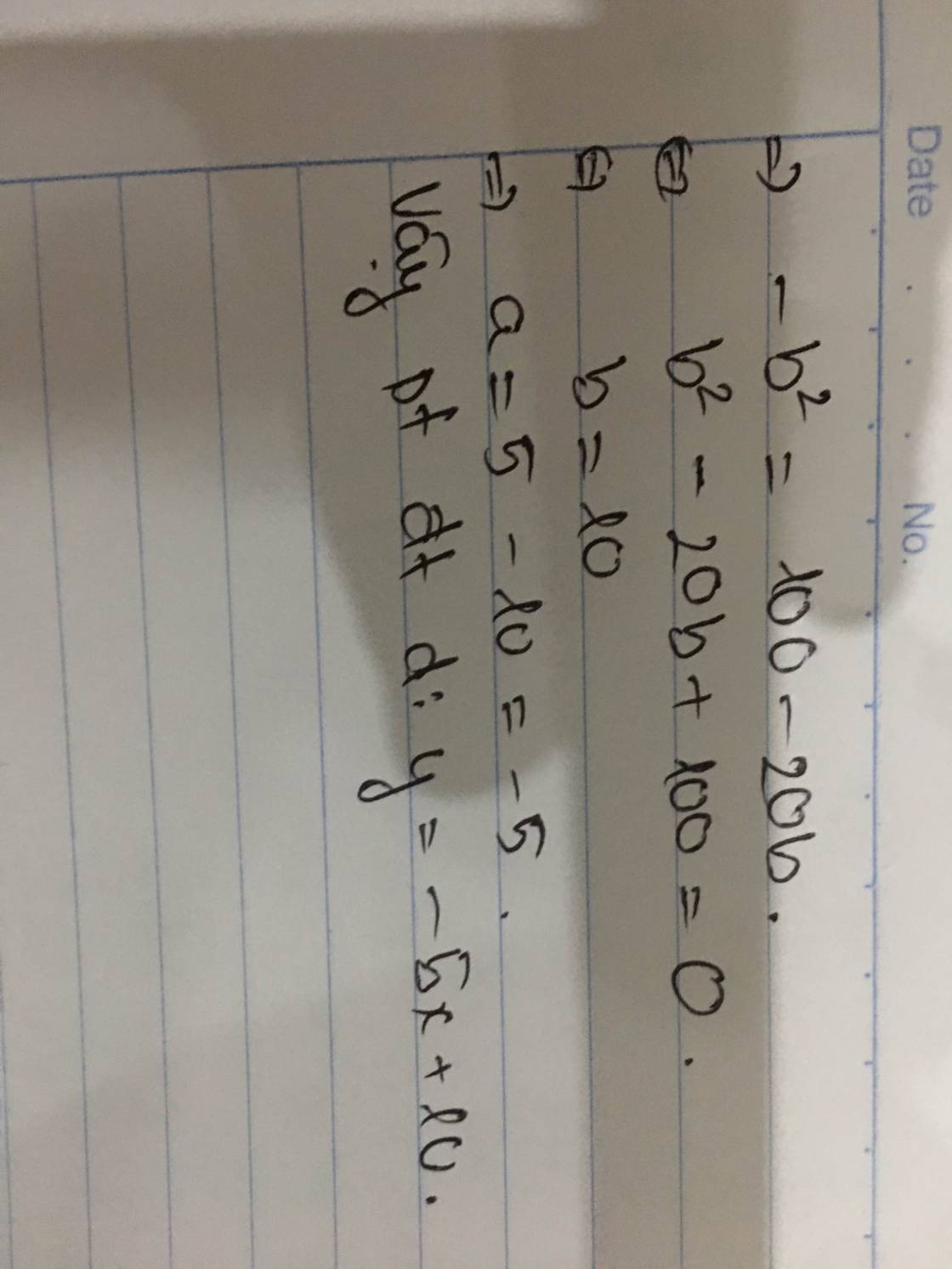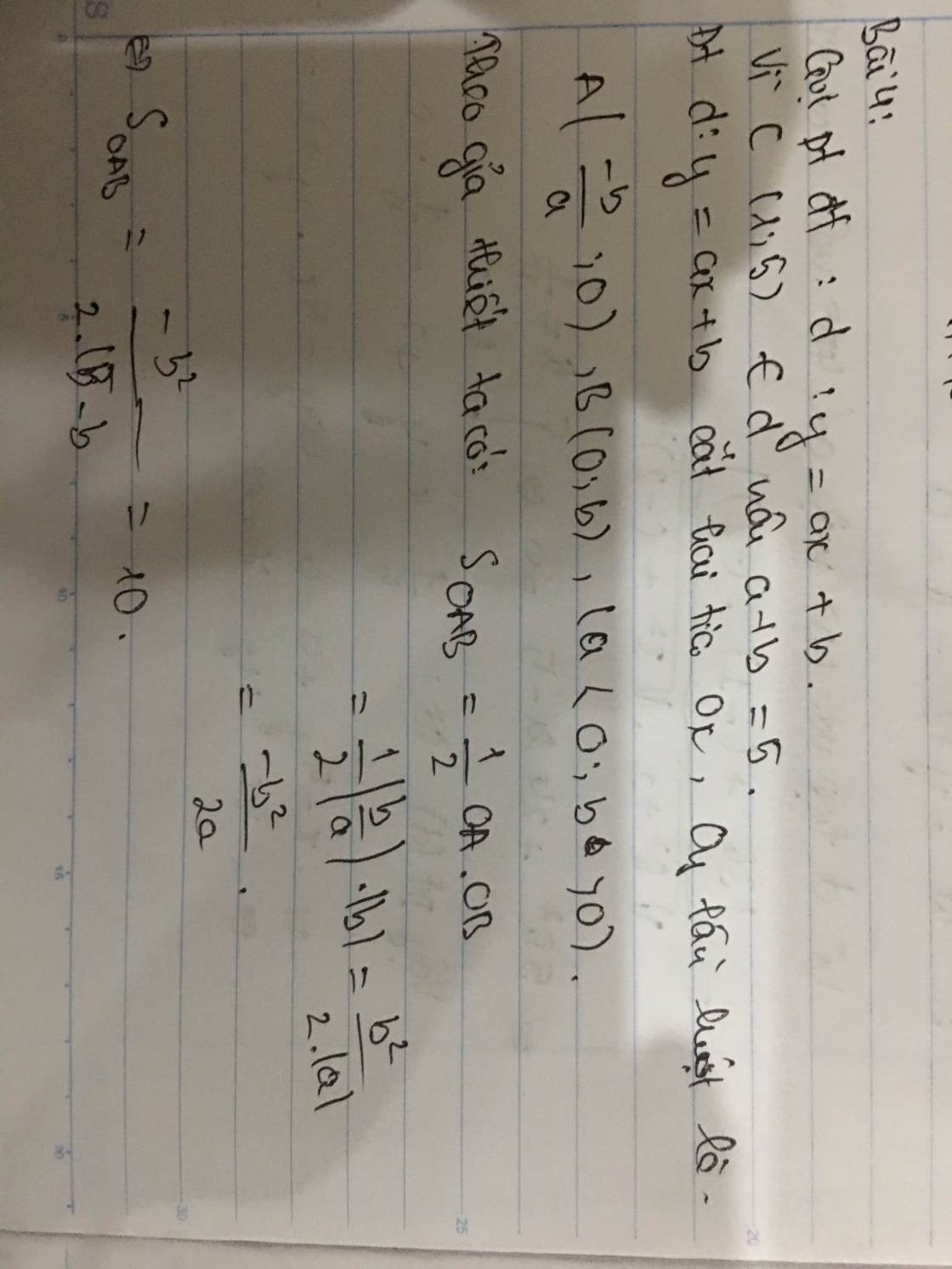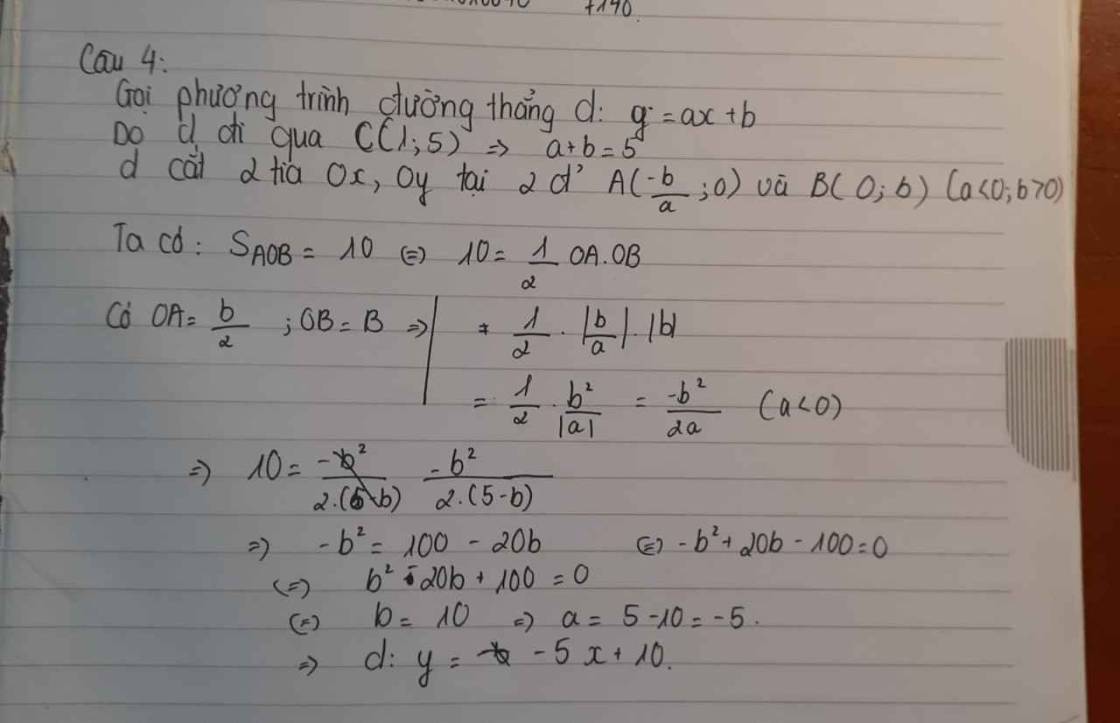Question

Trong mặt phẳng với hệ trục toạ độ $Oxy$, cho đường thẳng $d$ đi qua điểm $C\left( 1;5 \right)$ và $d$ tạo với hai tia $Ox$, $Oy$ một tam giác có diện tích bằng $10$. Viết phương trình đường thẳng $d$.

Answer 1

Answer 2

    

Answer 3

Do d qua C nên pt d có dạng: $y=kx-k+5$ (với $\mathrm{k\backslash (\backslash ne0;5\backslash ))}$
Gọi A và B lần lượt là giao điểm của d với Ox; Oy
\(=>\left\{{}\begin{matrix}(\dfrac{k-5}{k};0)\\(0;-k+5)\end{matrix}\right.\) 
Để A; B có hoành độ dương (do nằm trên các tia Ox; Oy) =>k<0
Khi đó: OA = \(\dfrac{k-5}{k};OB=-k+5\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\)10<=>\(\dfrac{\left(k-5\right)\left(-k+5\right)}{k}=20\)
=>\(k^2+10k+25=0\) =>k=-5
Phương trình d: $y=-5x+10$

 

 

 

Answer 4

  

Answer 5

  

Answer 6

  

Answer 7

  

Answer 8

  

Answer 9

  

Answer 10

    

Answer 11

  

Answer 12

  

Answer 13

  

Answer 14

  

Answer 15

Answer 16

Phương trình đường thẳng d:y=-5x+10

Answer 17

  

Answer 18

  

Answer 19

Answer 20

Answer 21

  

Answer 22

  

Answer 23

  

Answer 24

  

Answer 25

  

Answer 26

    

Answer 27

File: undefined 

Answer 28

d; y=-5x10

Answer 29

Answer 30