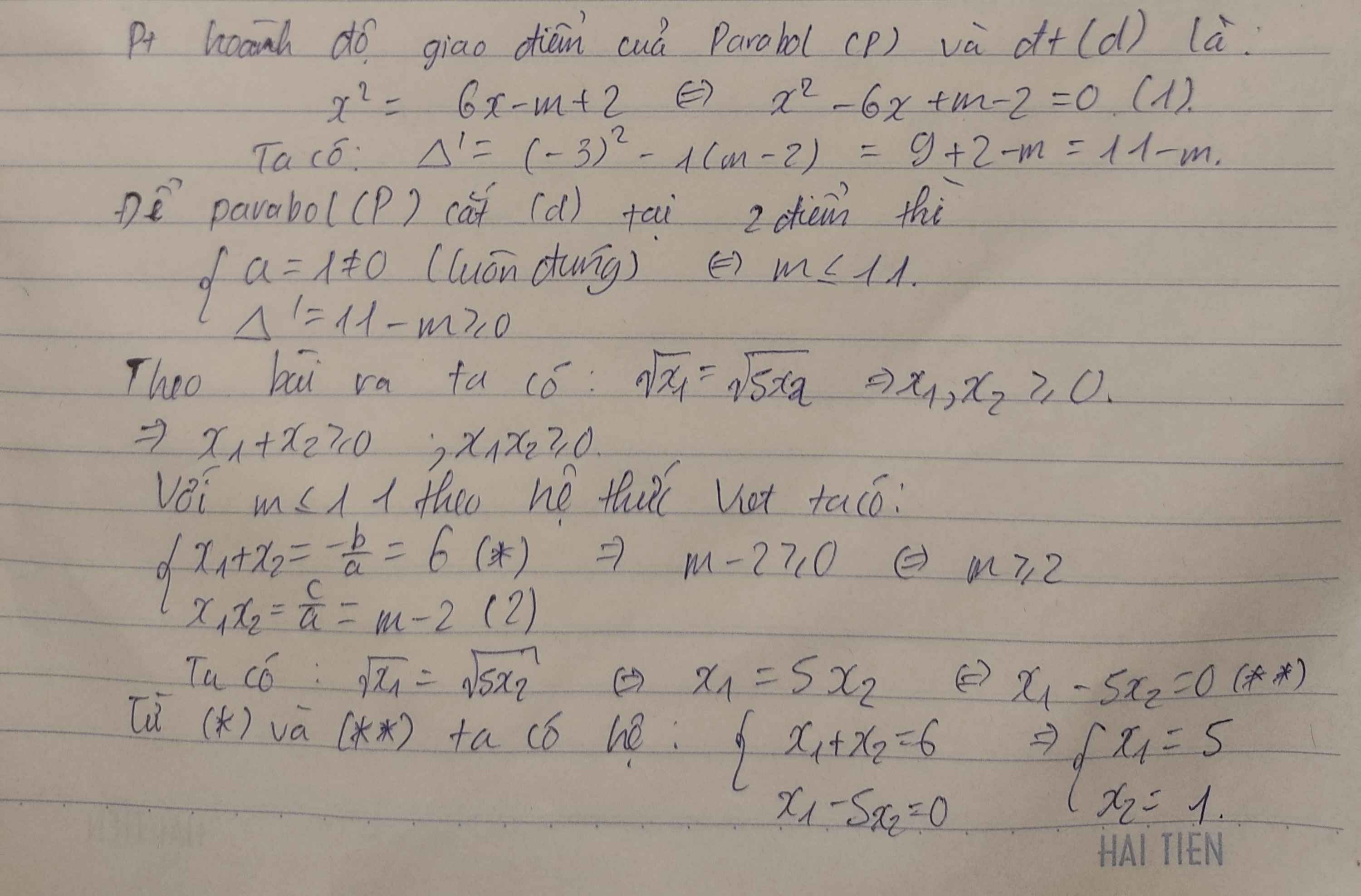Các câu hỏi tương tự
Trong mặt phẳng tọa độ Ãy cho parapol (P): y=\(x^2\) và đường thẳng (d): y=mx+1-m.
a) Xác định tọa độ giao điểm của (P) và (d) khi m=-1
b) Tìm m để (P) và (d) cắt nhau tại 2 điểm phân biệt có hoàng độ \(x_1\);\(x_2\) thỏa mãn \(\sqrt{x_1}+\sqrt{x_2}=3\)
Trong mặt phẳng tọa độ Oxy, cho parabol (P):y=`x^2` và `(d):y=2mx+2m+8`
a) Khi `m=-4`, tìm tọa độ giao điểm của (d) và (P)
b) CMR: (d) và (P) luôn cắt nhau ở 2 điểm phân biệt có hoành độ `x_1 ,x_2`. Tìm m để `x_1 +2x_2 =2`
Trong mặt phẳng tọa độ Oxy, cho parabol (p) : y-dfrac{x^2}{2}và đường thẳng (d): yx+ma) Tìm tọa độ điểm M thuộc parabol (P) biết điểm M có tung độ bằng -2b,Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm Aleft(x_1,M_1right),Bleft(x_2,y_2right)phân biệt thỏa mãn x_1x_2+x_1+x_210giúp mk câu này với ạ
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho parabol (p) : y=\(-\dfrac{x^2}{2}\)và đường thẳng (d): y=x+m
a) Tìm tọa độ điểm M thuộc parabol (P) biết điểm M có tung độ bằng -2
b,Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm A\(\left(x_1,M_1\right)\),B\(\left(x_2,y_2\right)\)
phân biệt thỏa mãn \(x_1x_2+x_1+x_2=10\)
giúp mk câu này với ạ
Trong mặt phẳng tọa độ Oxy cho parabol ( P):y= \(x^2
\) và đường thẳng
( d) : y= \(2(m+1)x-m^2-2\)(m là tham số)
Tìm các giá trị của m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ \(x^1,x^2\) sao cho \(x_1^2+x_1x_2+2=3x_1+x_2\)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx + m + 1 (m là tham số) và parabol (P): y = x2. Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho x1 + x2 + x1x2 = \(\sqrt{x_2}-\sqrt[3]{7-x_1}\)
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d):y=2x-2m+2 và parabol (P):y=x^2
a,Xác định các tọa độ giao điiểm của parabol (P)tại 2 điểm (d) khi m=-1/2
b,Tìm m để đường thẳng (d) vắt parabol (P) tại 2 điểm phân biệt \(A\left(x;y\right);B\left(x_2;y_2\right)\) sao cho \(y_1+y_2=4\left(x_1+x_2\right)\)
Trong mặt phẳng tọa độ Oxy có đường thẳng d: \(y=mx\)va parabol P: \(y=x^2\)
Tìm m để d cắt P tại 2 điểm phân biệt có hoành độ thỏa mãn: \(4\text{(\frac{1}{x_1}+\frac{1}{x_2})-x_1x_2+3=0}\)
Trong mặt phẳng tọa độ Oxy cho parabol (P): ydfrac{1}{2}x^2 và đường thẳng (d): y2x-m+1 ( Với m là tham số )a, Tìm m để đường thẳng (d) đi qua điểm A(-1;3) b, Tìm m để (d) cắt (P) tại hai điểm phân biệt có tọa độ left(x_1;y_1right):left(x_2;y_2right) sao cho x_1x_2left(y_1+y_2right)+480
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho parabol (P): \(y=\dfrac{1}{2}x^2\) và đường thẳng (d): \(y=2x-m+1\) ( Với m là tham số )
a, Tìm m để đường thẳng (d) đi qua điểm A(-1;3)
b, Tìm m để (d) cắt (P) tại hai điểm phân biệt có tọa độ \(\left(x_1;y_1\right):\left(x_2;y_2\right)\) sao cho \(x_1x_2\left(y_1+y_2\right)+48=0\)
câu 2: cho parabol (P):\(y=x^2\) và đường thẳng(d): \(y=2x+m\)(m là tham số)
a)tìm tọa độ giao điểm của (d) và (P) khi m=3
b)tìm m để (d) cắt (P) tại 2 điểm phân biệt thỏa mãn : \(x_1^2+x^2_2+x_1+x_2=2020\)
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) y=2x2-a2 và parabol (P) y=ax2(trong đó a là tham số dương)
a) Tìm a để (d) và (P) cắt nhau tại hai điểm A và B. CMR khi đó A và B có hoành độ dương
b) Tìm a để thỏa mãn bt sau :
\(\frac{1}{x_1+x_2}+\frac{1}{x_1.x_2}=3\)