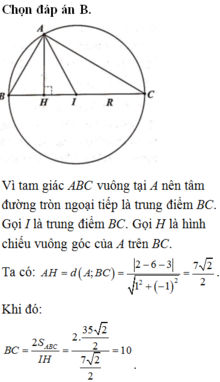
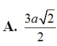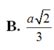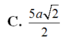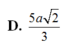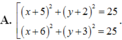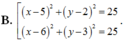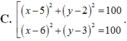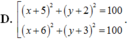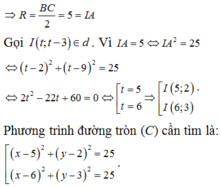Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxy cho tam giác ABC biết A(1;0;-1), B(2;3;-1), C(-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng (ABC). A.
x
-
3
3
y
-
1
-...
Đọc tiếp
Trong không gian tọa độ Oxy cho tam giác ABC biết A(1;0;-1), B(2;3;-1), C(-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng (ABC).
A. x - 3 3 = y - 1 - 1 = z - 5 5
B. x 3 = y - 2 1 = z 5
C. x - 1 1 = y - 2 = z + 1 2
D. x - 3 3 = y - 2 1 = z 5
Trong mặt phẳng tọa độ Oxy, cho đường tròn
(
C
2
)
:
x
2
+
y
2
-
12
x
+
18
0
và đường thẳng d:x-y+4. Phương trình đường tròn có tâm thuộc (
C
2
), tiếp xúc với d và cắt (
C
1
) tại hai điểm phân biệt A và B sao c...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C 2 ) : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d:x-y+4. Phương trình đường tròn có tâm thuộc ( C 2 ), tiếp xúc với d và cắt ( C 1 ) tại hai điểm phân biệt A và B sao cho AB vuông góc với d là
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
A
.
x
3
y
-
2
-
1
z
5
B
.
...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
A . x 3 = y - 2 - 1 = z 5
B . x 3 = y - 2 1 = z 5
C . x - 1 1 = y - 2 = z + 1 2
D . x - 3 3 = y - 2 - 1 = z - 5 5
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
3
y
-
2
z
+
12
0
. Gọi A, B, C lần lượt là giao điểm của
α
với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
α
có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + 3 y - 2 z + 12 = 0 . Gọi A, B, C lần lượt là giao điểm của α với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với α có phương trình là
![]()
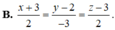
![]()
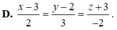
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
Đọc tiếp
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
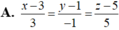
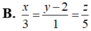
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng
(
α
)
: 2x + 3y - 2z + 12 0. Gọi A, B, C lần lượt là giao điểm của
(
α
)
với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
(
α
)
có phương trình là A.
x
-
3
2
y
-
2
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2x + 3y - 2z + 12= 0. Gọi A, B, C lần lượt là giao điểm của ( α ) với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với ( α ) có phương trình là
A. x - 3 2 = y - 2 3 = z - 3 - 2
B. x + 3 2 = y - 2 - 3 = z - 3 2
C. x + 3 2 = y + 2 3 = z - 3 - 2
D. x - 3 2 = y - 2 3 = z + 3 - 2
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
M
(
2
;
0
)
là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là
7
x
-
2
y
-
3
0
và
6
x
-
y
-
4
0
. Phương trình đường thẳng AC...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
Trong mặt phẳng (P) cho tam giác OAB cân tại O, OAOB2a,
A
O
B
⏜
120
0
. Trên đường thẳng vuông góc với măt phẳng (P)tại O lấy hai điểm C, D, nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
Đọc tiếp
Trong mặt phẳng (P) cho tam giác OAB cân tại O, OA=OB=2a, A O B ⏜ = 120 0 . Trên đường thẳng vuông góc với măt phẳng (P)tại O lấy hai điểm C, D, nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.