Chọn B.
Gọi ∆ là trung trực của đoạn OM
![]() ∆
qua trung điểm I của OM
∆
qua trung điểm I của OM
![]() I(2;1) và có vectơ pháp tuyến
I(2;1) và có vectơ pháp tuyến ![]()
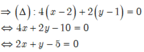
Chọn B.
Gọi ∆ là trung trực của đoạn OM
![]() ∆
qua trung điểm I của OM
∆
qua trung điểm I của OM
![]() I(2;1) và có vectơ pháp tuyến
I(2;1) và có vectơ pháp tuyến ![]()
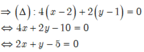
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
![]()
![]()
![]()
![]()
Cho z 1 , z 2 là hai trong các số phức z thỏa mãn điều kiện |z - 5 – 3i| = 5, đồng thời z 1 - z 2 = 0 . Tập hợp các điểm biểu diễn của số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây?
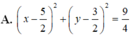
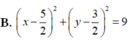
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d: x - 2 - 1 = y - 1 2 = z 2 và mặt phẳng (P): x+2y-z-5=0. Tọa độ giao điểm của d và (P) là
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x + 3 2 = y + 1 1 = z - 3 1 và mặt phẳng P : x + 2 y - z + 5 = 0 . Tìm tọa độ giao điểm M của đường thẳng d và mặt phẳng (P).
A. M(-1 ;0 ;4)
B. M(1 ;0 ;-4)
D. M(-5 ;-2 ;2)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
![]()
![]()
![]()
![]()
Xét các số phức z=x+yi x , y ∈ R có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình (C): x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
![]()
![]()
![]()
![]()
Cho mặt phẳng (P): x-2y+z+5=0. Viết phương trình mặt phẳng α vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
![]()
![]()
![]()
![]()
xét các vị trị tương đối của mỗi cặp phẳng cho bởi các phương trình sau.
a) x+2y-z+5=0 và 2x+3y-7z-4=0
b) x-2y+z-3=0 và 2x-y+4z-2=0
c) x+y+z-1=0 và 2x+2y+2z+3=0
d) 3x-2y+3z+5=0 và 9x-6y-9z-5=0
e) x-y+2z-4=0 và 10x-10y+20z-40=0