Dễ thấy u n = 4 n − 5
Ta có: u n + 1 = 4 ( n + 1 ) − 5 = 4 n − 1
⇒ u n + 1 = u n + 4 , ∀ n ≥ 1
Suy ra u n là một cấp số cộng với công sai là d = 4
Vậy u 1 + u 2 + ... + u 15 = S 15 = 15 2 u 1 + u 15 = 15 2 − 1 + 55 = 405
Đáp án là A
Dễ thấy u n = 4 n − 5
Ta có: u n + 1 = 4 ( n + 1 ) − 5 = 4 n − 1
⇒ u n + 1 = u n + 4 , ∀ n ≥ 1
Suy ra u n là một cấp số cộng với công sai là d = 4
Vậy u 1 + u 2 + ... + u 15 = S 15 = 15 2 u 1 + u 15 = 15 2 − 1 + 55 = 405
Đáp án là A
Cho hàm số y = 2 x 3 - 3 x 2 + 1 có đồ thị (C) và đường thẳng d : y = x - 1 . Số giao điểm của (C) và d là
A. 1
B. 3
C. 0
D. 2
cho hàm số y = \(\frac{^{x^2-2mx+3m-2}}{x-1}\)
a. Tìm các tiếp tuyến của đồ thị hàm số tại giao điểm đồ thị và Ox vuông góc với nhau
b. Pt y'=0 có 2 nghiệm x1,x2. Gọi A(x0;y0); B(x2;y2). Tìm M để k/c từ gốc toạ độ đến đường thẳng AB = \(\sqrt{2}\)
cho hàm số y=x^3+3x^2+1 có đồ thị (C)/.Gọi d là tiếp tuyến của C tại điểm A(1,5) và B la giao điểm thứ hai của d với C khi đó diện tích tam giác oab bằng
Cho hàm số \(y=-x^2+3x-2\) có đồ thị (D) a;Tính đạo hàm của hàm số tại điểm y',\(x_0\) thuộc R b,Viết phương trình tiếp tuyến của (P) tại điểm có hoành độ \(x_0=2\) c,Viết phương trình tiếp tuyến của (P) tại điểm có tung độ \(y_0=0\); d, Viết phương trình tiếp tuyến của (P) biết tiếp tiếp vuông góc với đường thẳng y'=x+3
Cho hàm số y = x 3 - 2 x 2 + ( m - 1 ) x + 2 m có đồ thị là C m . Tìm m để tiếp tuyến của đồ thị C m tại điểm có hoành độ x = 1 song song với đường thẳng (d): y = 3x +100.
A. m = 2
B. m = 4
C. m = 5
D. Không tồn tại m
Cho dãy hình vuông H1, H2, ... , Hn với mỗi số nguyên dương n, gọi un, pn và sn lần lượt là độ dài cạnh , chu vi và diện tích hình vuông Hn .
a) Giả sử dãy số (un )là một cấp cộng với công sai khác 0. Hải khi đó các dãy số (pn ) và (sn) có phải các cấp số cộng hay không? Vì sao?
b) Giả sử (un)là một cấp số nhân với công bội dương. Hỏi khi đó các dãy số (pn) và (sn)có phải là các cấp số nhân hay không? vì sao?
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là (C).Giả sử (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2, đồng thời (d) cắt đồ thị (C) tại N, tìm tọa độ N.
A. N(1;-1)
B. N(2;3)
C. N(-4;-51)
D. N(3;19)
Trong mặt phẳng Oxy , cho hình bình hành ABCD với A(3;2) ; D(4;1). Biết điểm B di động trên đường tròn (C):(x-2)^2+(y+1)^2=32 điểm C thuộc đường thẳng (d):x+y-1=0 .Biết rằng C có hoành độ dương . Tọa độ điểm C là
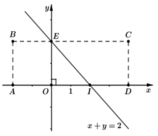
Trên mặt phẳng O x y ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0) (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y < 2
A. 1 3
B. 8 21
C. 3 7
D. 4 7