Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:
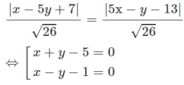
Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:
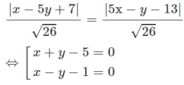
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x − 5y + 7 = 0 và đường thẳng d’ có phương trình 5x – y – 13 = 0. Tìm phép đối xứng trục biến d thành d’.
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình: x − 2y + 2 = 0 và d đường thẳng có phương trình: x − 2y – 8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình
A. 3x + 3y - 2 = 0
B. x - y + 2 = 0
C. x + y + 2 = 0
D. x + y - 3 = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-2y+2=0 và đường thằng l có phương trình : x - y + 1 = 0. Phép đối xứng trục l biến d thành d’ có phương trình
A. 2x - y - 1 = 0
B. 2x - y + 1 = 0
C. 2x + y + 1 = 0
D. 2x + y - 1 = 0
Trong mặt phẳng Oxy, cho đường thẳng d:x-2y+2=0; d':x-2y-8=0 Phép đối xứng tâm biến d thành d' và biến trục Ox thành chính nó có tâm I là:
A. (0;-3)
B. (0;3)
C. (-3;0)
D. (3,0)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x - 2y + 2 = 0; đường thẳng d’ có phương trình x - 2y - 8 = 0. Tìm tọa độ điểm I sao cho phép đối xứng tâm I biến d thành d’ đồng thời biến trục Oy thành chính nó.
A. I(-2;0)
B. I(8;0)
C. I(-3/2;0)
D. I(0; -3/2)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
A. x - 2y + 4 = 0
B. x + 2y + 4 = 0
C. 2x + y + 2 = 0
D. 2x - y + 4 = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1). Phép đối xứng tâm I biến d thành d’ có phương trình:
A. 6x - 5y - 7 = 0
B. 6x + 5y - 7 = 0
C. 6x - 5y + 7 = 0
D. 6x + 5y + 7 = 0
Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x - y - 1 = 0 thành đường thẳng d’ có phương trình.
A. x - y + 3 = 0
B. x + y - 3 = 0
C. x + y + 3 = 0
D. x - y + 2 = 0