Tam giác cân có trục đối xứng là đường cao (cũng là trung trực, phân giác).
Đáp án D
Tam giác cân có trục đối xứng là đường cao (cũng là trung trực, phân giác).
Đáp án D
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
A. S A ⊥ A B C
B. O ∈ S H
C. S A H ⊥ S B C
D. S B C , A B C ^ = S B A ^
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a Cạnh bên SA vuông góc với mặt phẳng đáy. Trong các tam giác sau, tam giác nào không phải là tam giác vuông?
A. △ S A B
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a.
A . a 3 3
B . 2 a 3
C . a 3 2
D . a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC= a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh 2 3 a . Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là a 3 , tính góc giữa SA và mặt phẳng (SBC).
A. π 6
B. π 3
C. π 4
D. a r c tan 3 2
Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm, đối xứng?
Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a, diện tích xung quanh của hình nón là:
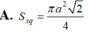
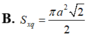
![]()
![]()
Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyến bằng a, diện tích xung quanh của hình nón đó là:
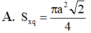

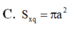

Tính thể tích hình chóp S.ABCD có đáy là hình thoi cạnh a, B A D ^ = 45 0 biết tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy
A. a 3 2
B. a 3 6
C. a 3 2 2
D. a 3 2 12