Đáp án B
Phương pháp
Đường thẳng d có VTCP u → và đi qua điểm M

Cách giải
Ta có
![]()
![]()

Đáp án B
Phương pháp
Đường thẳng d có VTCP u → và đi qua điểm M

Cách giải
Ta có
![]()
![]()

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;0;0), B(0;3;1), C(-1;4;2). Độ dài đường cao đỉnh A của tam giác ABC
A. 6
B. 2
C. 3 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết A (2;0;0), B (0;2;0), C (1;1;3). Gọi H ( x 0 ; y 0 ; z 0 ) là chân đường cao hạ từ đỉnh A xuống BC. Khi đó x 0 + y 0 + z 0 bằng bao nhiêu?
A. 38 9
B. 34 11
C. 30 11
D. 11 34
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;1;2), B(-2;3;1), C(3;-1;4). Viết phương trình đường cao của tam giác ABC kẻ từ đỉnh B
A. x = - 2 - t y = 3 + t z = 1 - t
B. x = - 2 + t y = 3 z = 1 - t
C. x = 1 + 2 t y = 3 + t z = 1 + t
D. x = - 2 + t y = 3 - t z = 1 + t
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;2;-2), B(-3;5;1), C(1;1;-2).Tìm toạ độ trọng tâm G của tam giác ABC ?
A. G(0;2;-1)
B. G(0;2;3)
C. G(0;-2;-1)
D. G(2;5;-2)
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A(1;-3;4), B(-2;-5;-7) và C(6;-3;-1). Phương trình đường trung tuyến AM của tam giác ABC là:
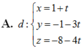
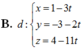
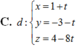
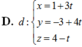
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(-2;0;0), B(0;3;0) và C(0;0;2). Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
![]()
![]()
![]()
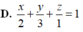
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;-2;2), B(-5;6;4), C(0;1;-2). Độ dài đường phân giác trong của góc A của ∆ ABC là:
A. 3 74 2
B. 3 2 74
C. 2 2 74
D. 2 74 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A ( 1 ; 2 ; - 1 ) , B ( 2 ; - 1 ; 3 ) , C ( - 2 ; 3 ; 3 ) . Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC
A. D(0;3;1).
B. D(0;1;3)
C. D(0;-3;1).
D. D(0;3;-1).