Đáp án B:
Ta có: Oz ⊥ (Oxy) nên nhận vecto k ⇀ = (0, 0, 1) làm vecto pháp tuyến của (Oxy)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+3y-4z-50. Vectơ nào dưới đây là một vectơ pháp tuyến của (P) A.
n
1
→
(
2
;
-
3
;
4
)
B. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+3y-4z-5=0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)
A. n 1 → = ( 2 ; - 3 ; 4 )
B. n 2 → = ( 2 ; 3 ; 4 )
C. n 3 → = ( 2 ; 4 ; 5 )
D. n 4 → = ( 2 ; - 3 ; - 5 )
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 3x - z + 2 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A. (3;-1;2)
B. (-1;0;1)
C. (3;0;-1)
D. (3;-1;0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
P
:
x
3
+
y
2
+
z
1
1
. Vectơ nào dưới đây là vectơ pháp tuyến của (P)?
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x 3 + y 2 + z 1 = 1 . Vectơ nào dưới đây là vectơ pháp tuyến của (P)?
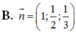
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - 3z + 2 = 0. Vectơ nào dưới đây là vectơ pháp tuyến của (P)
A. (-2;3;0)
B. (2;-3;1)
C. (2;-3;2)
D. (2;0;-3)
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) có phương trình
y
−
z
+
2
0
. Vectơ nào dưới đây là vectơ pháp tuyến của (P)? A.
n
→
(
1
;
−
1
;
2
)
.
B.
n
→
(
1
;
−
1
;
0
)
....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) có phương trình y − z + 2 = 0 . Vectơ nào dưới đây là vectơ pháp tuyến của (P)?
A. n → = ( 1 ; − 1 ; 2 ) .
B. n → = ( 1 ; − 1 ; 0 ) .
C. n → = ( 0 ; 1 ; − 1 ) .
D. n → = ( 0 ; 1 ; 1 ) .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(0;1;1); B(1;-2;0) và C(1;0;2). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P)
A. (-4;2;-2)
B. (2;-1;1)
C. (4;2;2)
D. (2;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;-2;0), C(0;0;-5). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (ABC)?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;-2;0), C(0;0;-5). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (ABC)?
Trong không gian với hệ tọa độ đề các vuông góc Oxyz, cho mặt phẳng (P): x-2y+2z-40. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P)?
Đọc tiếp
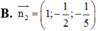
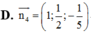
Trong không gian với hệ tọa độ đề các vuông góc Oxyz, cho mặt phẳng (P): x-2y+2z-4=0. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P)?
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - 4y + 7 = 0.
Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng (P)?
A. (2;-4;7)
B. (1;-2;0)
C. (2;4;0)
D. (-3;2;-1)