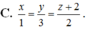Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 và hai đường thẳng d 1 : x - 5 1 = y + 1 1 = z - 1 2 ; d 2 : x + 1 1 = y 2 = z 1 ; Viết phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu (S) đồng thời song song với hai đường thẳng d 1 , d 2
A. α : 3x-y-z-15=0
B. α : 3x-y-z+7=0
C. α : 3x-y-z-7=0
D. α : 3x-y-z+7 =0 hoặc α : 3x-y-z-15=0
Đáp án B
Mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 có tâm I(1;-1;0) bán kính R= 11
Các đường thẳng d 1 , d 2 có vectơ chỉ phương lần lượt là:
![]()
Mặt phẳng α song song với d 1 , d 2 có vectơ pháp tuyến là:
![]()
α có dạng: α : 3x-y-z+d=0. Vì α tiếp xúc với (S ) nên: d(I; α )=R
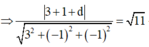
![]()
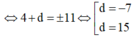
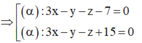
Nhận thấy điểm A(5;-1;1) ∈ d 1 cũng thuộc vào mặt phẳng 3x-y-z+15=0 =>mặt phẳng này chứa d 1
Vậy phương trình mặt phẳng α thỏa mãn yêu cầu bài toán là: α : 3x-y-z+7=0