Đáp án là B.
![]()
Ta có:
![]()
![]()
Tam giác ABM vuông tại A.
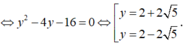
Đáp án là B.
![]()
Ta có:
![]()
![]()
Tam giác ABM vuông tại A.
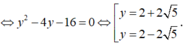
Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho △ A B M vuông tại M.
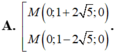
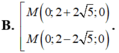
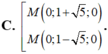
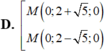
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B →
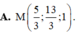
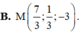
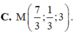
![]()
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:

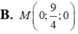
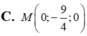

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M(1;3;-2), cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho O A 1 = O B 2 = O C 4
A. x+2y+4z+1=0
B. 4x+2y+z-8=0
C. 2x-y-z-1=0
D. 4x+2y+z+1=0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 = 9 , điểm M(1;1;2) và mặt phẳng (P): x+y+z-4=0 . Gọi ∆ là đường thẳng đi qua M, thuộc (P) và cắt (S) tại hai điểm A, B sao cho AB nhỏ nhất. Biết rằng ∆ có một vecto chỉ phương là u ⇀ (1;a;b), tính T=a-b
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A, B với O A → = ( 2 ; - 1 ; 3 ) , O B → = = ( 5 ; 2 ; - 1 ) . Tìm tọa độ của vectơ A B → .
![]()
![]()
![]()
![]()
Trong không gian hệ tọa độ Oxyz, cho tứ diện ABCD với A(2;3;2), B(6;-1;-2), C(-1;-4;3), D(6;-1;-2). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất.
A. M(1;1;0)
B. M(0;1;-1)
C. M(1;1;-1)
D. M(-1;1;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(3;2;-1), B(5;4;3). M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 . Tìm tọa độ của điểm M.
A. (7;6;7)
B. 13 3 ; 10 3 ; 5 3
C. - 5 3 ; - 2 3 ; 11 3
D. (13;11;5)