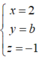
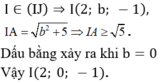
Chọn C
Gọi J là trung điểm AB = > J = (2;0;-1)
Tam giác ABO vuông tại O nên J là tâm đường tròn ngoại tiếp tam giác OAB. Gọi I là tâm mặt cầu (S), (S) qua các điểm A, B, O. Ta có đường thẳng IJ qua J và có một VTCP là 
nên có PTTS: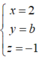 
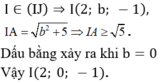
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;0;-2), B(4;0;0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là
A. I(2;0;-1)
B. I(0;0;-1)
C. I(2;0;0)
D. I 4 3 ; 0 ; - 2 3
Trong không gian với hệ tọa độ cho ba điểm A(−2;0;0), B(0;−2;0)và C(0;0;−2). Gọi D là điểm khác O sao cho DA,DB,DC đôi một vuông góc với nhau và I(a;b;c) là tâm mặt cầu ngoại tiếp tứ diện ABCD.Tính S=a+b+c
A. S= -3
B. S= -1
C. S= -2
D. S= -4
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1;-2;0), B(0;-4;0), C(0;0;-3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. 6x-3y+5z=0
B. -6x+3y+4z
C. 2x-y-3z=0
D. 2x-y+3z=0
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
Trong không gian Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) di động trên các trục Ox, Oy, Oz sao cho 2a+b-c-6=0 và hai điểm M(2;-3;5). Xét các mặt cầu (S) ngoại tiếp tứ diện OABC có tâm I. Khi 2 I M → + I N → đạt giá trị nhỏ nhất thì mặt cầu (S) có diện tích bằng
A. 14 π .
B. 64 π .
C. 56 π .
D. 16 π .
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c là các số thực thay đổi thỏa mãn 1 a - 1 b + 1 c = 1 . Biết rằng mặt cầu S : x - 2 2 + y - 1 2 + z - 3 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a+b-c bằng
Trong không gian Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 48 Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C). Khối nón (N) có đỉnh là tâm của (S), đường tròn đáy là (C) cỏ thể tích lớn nhất bằng
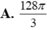
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-3=0. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S).
A. R=3.
B. R=9
C. R=1
D. R=5.
Trong không gian với hệ trục tọa độ Oxyz, cho các mặt cầu (S1), (S2), (S3) có bán kính r=1 và lần lượt có tâm là các điểm A(0;3;-1), B(-2;1;-1), C(4;-1;-1). Gọi (S) là mặt cầu tiếp xúc với cả ba mặt cầu trên. Mặt cầu (S) có bán kính nhỏ nhất là
