Đáp án A
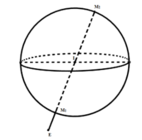
Mặt cầu (S) có tâm I(1;1;1). Gọi E là điểm thoả mãn
![]()
![]()
T nhỏ nhất khi ME nhỏ nhất <=> M là 1 trong 2 giao điểm của đường thẳng IE và mặt cầu (S).
![]()
![]()
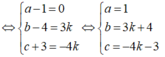
![]()
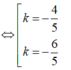
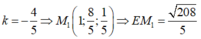
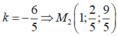
![]()
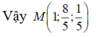
Đáp án A

Mặt cầu (S) có tâm I(1;1;1). Gọi E là điểm thoả mãn
![]()
![]()
T nhỏ nhất khi ME nhỏ nhất <=> M là 1 trong 2 giao điểm của đường thẳng IE và mặt cầu (S).
![]()
![]()
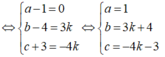
![]()
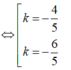
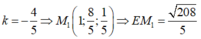
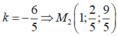
![]()
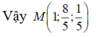
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
A. 2
B. 6
C. 6
D. 2
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A 0 ; 1 ; 1 , B 3 ; 0 ; − 1 , C 0 ; 21 ; − 19 và hai mặt cầu S : x − 1 2 + y − 1 2 + z − 1 2 = 1 . M a , b , c là điểm thuộc mặt cầu (S) sao cho biểu thức T = 3 M A 2 + 2 M B 2 + M C 2 đạt giá trị nhỏ nhất. Tính tổng a+b+c
A. 14 5
B. 0
C. 12 5
D. 12
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 9 và điểm M ( a ; b ; c ) ∈ ( S ) sao cho biểu thức P=2a+2b+2c đạt giá trị nhỏ nhất. Tính T=a+b+c.
A. 2
B. 1
C. -2
D. -1
Trong không gian Oxyz cho hai điểm A(2;-3;2), B(-2;1;4) và mặt cầu ( S ) : ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 12 . Điểm M(a,b,c) thuộc mặt cầu (S) sao cho M A → . M B → nhỏ nhất, tính a+b+c
A. 7 3
B. -4
C. 1
D. 4
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(8;5;-11), B(5;3;-4), C(1;2;-6) và mặt ( S ) : ( x - 2 ) 2 + ( y - 4 ) 2 + ( z - 1 ) 2 = 9 . Gọi điểm M(a;b;c) là điểm trên (S) sao cho M A → - M B → - M C → đạt giá trị nhỏ nhất. Hãy tìm a+b
A. 6
B. 2
C. 4
D. 9
Trong không gian tọa độ oxyz, cho mặt cầu (S): (x-1)^2+(y-2)^2+(z+3)^2=6 và hai điểm B(2;3;-1) và C(0;1;-5). Điểm A thuộc mặt cầu (S) sao cho AB<AC. Tia phân giác trong của góc BAC cắt mặt cầu (S) tại K. Hình chiếu của A trên đường thẳng BC là điểm H(a;b;c). Biết AH/AK= căn 15/17, khi đó a+b+c bằng
Trong không gian Oxyz, cho điểm A(1;−3;0) và mặt cầu (S): ( x - 2 ) 2 + ( y + 6 ) 2 + z 2 = 50 tâm I. Xét các điểm M thuộc (S) sao cho góc ∠ A M I lớn nhất, M luôn thuộc mặt phẳng có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + ( y - 2 ) 2 + z - 3 2 = 16 và các điểm A (1; 0; 2), B (-1; 2; 2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của (P) với mặt cầu (S) có diện tích nhỏ nhất.Khi viết phương trình (P) dưới dạng (P): ax + by + cz + 3 = 0. Tính T = a + b + c
A. 3
B. -3
C. 0
D. -2