Đáp án C
Vecto đơn vị trong hệ trục Oxyz: ![]()
Tọa độ điểm M trong không gian Oxyz: ![]()
Cách giải
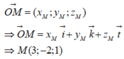
Đáp án C
Vecto đơn vị trong hệ trục Oxyz: ![]()
Tọa độ điểm M trong không gian Oxyz: ![]()
Cách giải
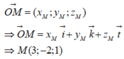
Trong không gian với hệ tọa độ ( O , i ⇀ , j ⇀ , k ⇀ ) cho 2 điểm A,B thỏa mãn O A ⇀ = 2 i ⇀ - j ⇀ + k ⇀ và O B ⇀ = i ⇀ + j ⇀ - 3 k ⇀ . Tìm tọa độ trung điểm M của đoạn thẳng AB
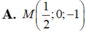
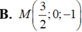
![]()
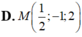
Trong không gian Oxyz, cho O A → = i → + j → - 3 k → , B 2 ; 2 ; 1 . Tìm tọa độ điểm M thuộc trục tung sao cho M A 2 + M B 2 nhỏ nhất
![]()
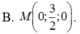
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, các véctơ đơn vị trên các trục Ox, Oy, Oz lần lượt là i → , j → , k → , cho điểm M(2;-1;1). Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho vectơ O M → = - j → + 5 k → . Khi đó tọa độ điểm M là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho O A → = 3 i → + j → - 2 k → và B(m;m-1;-4). Tìm tất cả giá trị của tham số m để độ dài đoạn AB=3
A. m=2 hoặc m=3
B. m=1 hoặc m=4
C. m=1 hoặc m=2
D. m=3 hoặc m=4
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(3;2;-1), B(5;4;3). M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 . Tìm tọa độ của điểm M.
A. (7;6;7)
B. 13 3 ; 10 3 ; 5 3
C. - 5 3 ; - 2 3 ; 11 3
D. (13;11;5)
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có A B → , A D → , A A ' → theo thứ tự cùng hướng với i → , j → , k → và có AB = a, AD = b, AA’ = c. Hãy tính tọa độ các vecto A B → , A C → , A C ' → v à A M → với M là trung điểm của cạnh C’D’.
Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho △ A B M vuông tại M.
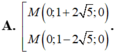
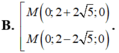
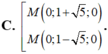
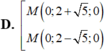
Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian tỏa mãn đẳng thức AM 2 + 2 BM 2 = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).
A. I(-1; -1; -4); R = 9
B. I(-2; -2; -8); R = 3
C. I(-1; -1; -4); R = 30 /2
D. I(-1; -1; -4); R = 3