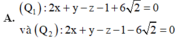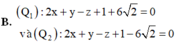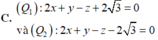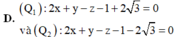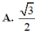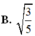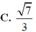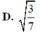Đáp án D
Phương pháp:
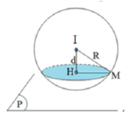
Trong đó
d: khoảng cách từ tâm O đến mặt phẳng (P),
r: bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P)
R: bán kính hình cầu.
Cách giải:
( S ) : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0
=> (S) có tâm I(3;-2;1) bán kính R = 3
(Q) cắt (S) theo giao tuyến là một đường tròn bán kính r = 2
Ta có
là một VTCP (Q)
Khi đó
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT n → =(0;b;c) là:
Khoảng cách từ tâm I đến (Q):
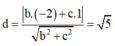
Phương trình mặt phẳng (Q): 2y -z =0
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
Trong không gian Oxyz , cho mặt cầu
( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 25 và mặt phẳng
( P ) : x - 2 y + 2 z + 8 = 0 . Biết (S) cắt (P) theo giao tuyến là một đường tròn có bán kính bằng
A. 3
B. 4
C. 1
D. 2
Trong không gian hệ tọa độ Oxyz cho mặt cầu (S): x 2 + y 2 + z 2 -2x + 2y - 4z -10 = 0 và mặt phẳng (P): 2x + y - z - 5 = 0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo đường tròn có bán kính bằng một nửa bán kính mặt cầu (S)
Cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y - 2z - 3 = 0 cắt 2 mặt phẳng (P): x - 2y + z = 0 và (Q): x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 ; r 2 . Khi đó tỉ số r 1 r 2 bằng
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : x 1 = y - 1 1 = z - 2 1 và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
A . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
B . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
C . S : x + 1 2 + y + 2 2 + z + 3 2 = 5
D . S : x - 1 2 + y - 2 2 + z - 3 2 = 3
Trong không gian Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 25 và mặt phẳng (P): x-2y+2z+8=0. Biết (S) cắt (P) theo giao tuyến là một đường tròn có thể tích bằng
A.3
B. 4
C. 1
D. 2
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
