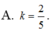Trong không gian \(Oxyz\), cho hai vecto \(\overrightarrow{u}\) và \(\overrightarrow{v}\) thỏa mãn \(\left|\overrightarrow{u}\right|=2;\left|\overrightarrow{v}\right|=1\) và \(\left(\overrightarrow{u},\overrightarrow{v}\right)=60^0\). Góc giữa hai vecto \(\overrightarrow{u}\) và \(\overrightarrow{u}-\overrightarrow{v}\)
\(\overrightarrow{u}.\left(\overrightarrow{u}-\overrightarrow{v}\right)=u^2-\overrightarrow{u}.\overrightarrow{v}=4-u.v.cos\left(u;v\right)=4-1=3\)
\(\Rightarrow cos\left(\overrightarrow{u};\overrightarrow{u}-\overrightarrow{v}\right)=\dfrac{\overrightarrow{u}.\left(\overrightarrow{u}-\overrightarrow{v}\right)}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{u}-\overrightarrow{v}\right|}\)(*)
Đặt \(A=\left|\overrightarrow{u}-\overrightarrow{v}\right|\)
\(A^2=\left(\overrightarrow{u}-\overrightarrow{v}\right)^2=u^2+v^2-2\overrightarrow{u}.\overrightarrow{v}=4+1-2.2.cos60^0=3\)
=> A = \(\sqrt{3}\)
Thay vào (*) ta được \(cos\left(\overrightarrow{u};\overrightarrow{u}-\overrightarrow{v}\right)=\dfrac{3}{2\sqrt{3}}=\dfrac{\sqrt{3}}{2}\Rightarrow\left(\overrightarrow{u};\overrightarrow{u}-\overrightarrow{v}\right)=30^0\)