Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;4;2) và mặt phẳng
α
: x+y+z-10 Tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng
α
là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;4;2) và mặt phẳng α : x+y+z-1=0 Tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng α là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, xác định tọa độ hình chiếu vuông góc của điểm M(2;3;1) trên mặt phẳng
α
: x-2y+z0. A.
2
;
5
2
;
3
B. (5;4;3) C. ...
Đọc tiếp
Trong không gian Oxyz, xác định tọa độ hình chiếu vuông góc của điểm M(2;3;1) trên mặt phẳng α : x-2y+z=0.
A. 2 ; 5 2 ; 3
B. (5;4;3)
C. 5 2 ; 2 ; 3 2
D. (1;3;5)
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
1.Cho điểm M(1 ; 4 ; 5) và mặt phẳng (α): x + y + z -1 =0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
: 3x-2y+z+60. Hình chiếu vuông góc của điểm A(2;-1;0) lên mặt phẳng
α
có tọa độ là A. (1;0;3) B. (-1;1;-1) C. (2;-2;3) D. (1;1;-1)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : 3x-2y+z+6=0. Hình chiếu vuông góc của điểm A(2;-1;0) lên mặt phẳng α có tọa độ là
A. (1;0;3)
B. (-1;1;-1)
C. (2;-2;3)
D. (1;1;-1)
Cho điểm M(1; -1; 2) và mặt phẳng ( α ): 2x – y + 2z + 12 = 0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng ( α )
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-40 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx là:
A
.
M
-
1
2
;
0
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
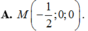
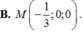
![]()
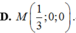
Trong không gian tọa độ Oxyz, cho ba điểm A(2;1;2), B(2;-3;1), C(3;2;2) và mặt phẳng
α
: x-3y+Z0. Gọi A, B, C lần lượt là hình chiếu vuông góc của A, B, C lên
α
. D là điểm sao cho ABCD là hình bình hành. Diện tích hình bình hành ABCD bằng A.
3
22
B.
4
11...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho ba điểm A(2;1;2), B(2;-3;1), C(3;2;2) và mặt phẳng α : x-3y+Z=0. Gọi A', B', C' lần lượt là hình chiếu vuông góc của A, B, C lên α . D' là điểm sao cho A'B'C'D' là hình bình hành. Diện tích hình bình hành A'B'C'D' bằng
A. 3 22
B. 4 11
C. 8 11
D. 6 22