Đáp án D
Phương trình mặt phẳng trung trực của AB là ( α ) : x + z + 1 = 0
Vì tam giác ABC đều ⇒ C ∈ ( α ) mà
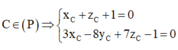
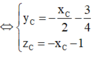
![]()
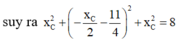
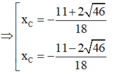
Vậy có 2 điểm C thỏa mãn yêu cầu bài toán.
Đáp án D
Phương trình mặt phẳng trung trực của AB là ( α ) : x + z + 1 = 0
Vì tam giác ABC đều ⇒ C ∈ ( α ) mà
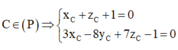
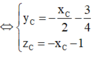
![]()
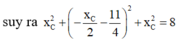
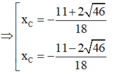
Vậy có 2 điểm C thỏa mãn yêu cầu bài toán.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1;-2;0), B(0;-4;0), C(0;0;-3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. 6x-3y+5z=0
B. -6x+3y+4z
C. 2x-y-3z=0
D. 2x-y+3z=0
Trong không gian với hệ trục tọa độ Oxyz ,cho 3 điểm A(1;0;0), B(0;-2;0), C(0;0;-5). Vectơ nào là một vectơ pháp tuyến của mặt phẳng (ABC)
A. 1 ; 1 2 ; 1 5
B. 1 ; - 1 2 ; - 1 5
C. 1 ; - 1 2 ; 1 5
D. 1 ; 1 2 ; - 1 5
Trong không gian tọa độ Oxyz, cho các điểm A (1; 2; 3), B (2; 1; 0), C (4; 3; -2), D (3; 4; 1), E (1; 1; -1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4
C. 5
D. Không tồn tại.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;-2;0), C(0;0;-5). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (ABC)?

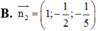

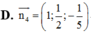
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c khác 0 Biết rằng mặt phẳng (ABC) đi qua điểm M 2 3 ; 4 3 ; 4 3 và tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 1 Thể tích khối tứ diện OABC bằng
A. 4
B. 6
C. 9
D. 12
Trong không gian tọa độ Oxyz cho các điểm A(1;2;3), B(2;1;0), C(4;-3;-2), D(3;-2;1), E(1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4
C. 5
D. không tồn tại
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-2;0), B (-3;2;-4) và mặt phẳng (P): x + 2y + z - 3 = 0.
Gọi M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho tam giác
MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị T = a 2 + b + c .
A. T = 1
B. T = 2
C. T = 0
D. T = 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
A. Có vô số mặt phẳng.
B. 1 mặt phẳng.
C. 7 mặt phẳng.
D. 4 mặt phẳng.