Các câu hỏi tương tự
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là: A. (P):x+2y+3z+60. B. (P):x+2y+z-20. C. (P):x-2y+z-60. D. (P):3x+2y+2z-40.
Đọc tiếp
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là:
A. (P):x+2y+3z+6=0.
B. (P):x+2y+z-2=0.
C. (P):x-2y+z-6=0.
D. (P):3x+2y+2z-4=0.
Trong không gian Oxyz cho hai đường thẳng
d
1
:
x
+
1
3
y
-
1
2
z
-
2
-
1
,
d
2
:...
Đọc tiếp
Trong không gian Oxyz cho hai đường thẳng d 1 : x + 1 3 = y - 1 2 = z - 2 - 1 , d 2 : x - 1 - 1 = y - 1 2 = z + 1 - 1 Đường thẳng ∆ đi qua điểm A(1;2;3) vuông góc với d 1 và cắt đường thẳng d 2 có phương trình là
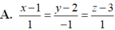
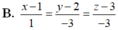
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
d
1
:
x
-
2
2
y
+
2
-
1
z
-
3
1
và
d
2
:
x
-
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 2 2 = y + 2 - 1 = z - 3 1 và d 2 : x - 1 - 1 = y - 1 2 = z + 1 1 . Phương trình đường thẳng ∆ đi qua điểm A(1;2;3) vuông góc với d1 và cắt d2 là:
A. x - 1 1 = y - 2 - 3 = z - 3 - 5
B. x - 1 1 = y + 2 - 3 = z + 3 - 5
C. x + 1 - 1 = y + 2 3 = z + 3 5
D. x - 1 1 = y + 3 - 2 = z + 5 - 3
Trong không gian Oxyz, cho các điểm A(1;-1;1), B(-1;2;3) và đường thẳng
d
:
x
+
1
-
2
y
-
2
1
z
-...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(1;-1;1), B(-1;2;3) và đường thẳng d : x + 1 - 2 = y - 2 1 = z - 3 3 . Đường thẳng ∆ đi qua điểm A, vuông góc với hai đường thẳng AB và d có phương trình là:
A. x - 1 2 = y + 1 4 = z - 1 7
B. x - 1 7 = y - 1 2 = z - 1 4
C. x - 1 2 = y + 1 7 = z - 1 4
D. x - 1 7 = y + 1 2 = z - 1 4
Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng (P) đi qua ba điểm
A
(
3
2
;
0
;
0
)
,
B
(
0
;
3
2
;
0
)
,
C
(
0
;
0
;
-
3
)
, và mặt cầu (S):
(
x
-
3
)
2
+...
Đọc tiếp
Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng (P) đi qua ba điểm A ( 3 2 ; 0 ; 0 ) , B ( 0 ; 3 2 ; 0 ) , C ( 0 ; 0 ; - 3 ) , và mặt cầu (S): ( x - 3 ) 2 + ( y - 2 ) 2 + ( z - 5 ) 2 = 36 . Gọi ∆ là đường thẳng đi qua điểm E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình ∆ là
A. x = 2 + 9 t y = 1 + 9 t z = 3 + 8 t
B. x = 2 - 5 t y = 1 + 3 t z = 3
C. x = 2 + t y = 1 - t z = 3
D. x = 2 + 4 t y = 1 + 3 t z = 3 - 3 t
Trong không gian oxyz phương trình đường thẳng d đi qua điểm M(3;0;-1) và có vecto chỉ phương a(-1;2;3) làA. left{{}begin{matrix}x3-ty2tz-1+3tend{matrix}right.B. left{{}begin{matrix}x-1+3ty2z3-tend{matrix}right.C. left{{}begin{matrix}x3+ty2tz-1-3tend{matrix}right.D. left{{}begin{matrix}x-1-3ty2z3+tend{matrix}right.
Đọc tiếp
Trong không gian oxyz phương trình đường thẳng d đi qua điểm M(3;0;-1) và có vecto chỉ phương a=(-1;2;3) là
A. \(\left\{{}\begin{matrix}x=3-t\\y=2t\\z=-1+3t\end{matrix}\right.\)
B. \(\left\{{}\begin{matrix}x=-1+3t\\y=2\\z=3-t\end{matrix}\right.\)
C. \(\left\{{}\begin{matrix}x=3+t\\y=2t\\z=-1-3t\end{matrix}\right.\)
D. \(\left\{{}\begin{matrix}x=-1-3t\\y=2\\z=3+t\end{matrix}\right.\)
Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3). Phương trình của mặt cầu có tâm I và đi qua A là: A.
(
x
+
1
)
2
+
(
y
+
1
)...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3). Phương trình của mặt cầu có tâm I và đi qua A là:
A. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 29
B. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 5
C. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 25
D. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 5
Trong không gian Oxyz, cho hai điểm A(1;2;3) và I(1;1;1). Phương trình của mặt cầu có tâm I và đi qua A là A.
(
x
+
1
)
2
+
(
y
+
1
)
2
+
(
z
+
1
)...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;2;3) và I(1;1;1). Phương trình của mặt cầu có tâm I và đi qua A là
A. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 29
B. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 5
C. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 25
D. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 5





