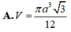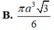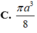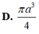Các câu hỏi tương tự
Trong không gian cho tam giác ABC là tam giác đều cạnh a. Gọi S là diện tích của mặt tròn xoay nhận được khi quay các cạnh AB và AC xung quanh trục BC. Tính S.
Đọc tiếp
Trong không gian cho tam giác ABC là tam giác đều cạnh a. Gọi S là diện tích của mặt tròn xoay nhận được khi quay các cạnh AB và AC xung quanh trục BC. Tính S.
![]()
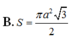
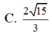
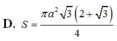
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số V 1 V 2 .
![]()
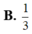
![]()
Trong không gian, cho tam giác ABC cân tại A,
A
B
a
10
,
B
C
2
a
Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH. A.
V
2
πa
3
B.
V
3
πa
3
C.
V
9
πa...
Đọc tiếp
Trong không gian, cho tam giác ABC cân tại A, A B = a 10 , B C = 2 a Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.
A. V = 2 πa 3
B. V = 3 πa 3
C. V = 9 πa 3
D. V = πa 3
Trong không gian, cho tam giác đều ABC cạnh bằng a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh một đường cao của nó.
Đọc tiếp
Trong không gian, cho tam giác đều ABC cạnh bằng a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh một đường cao của nó.
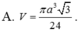
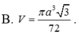
![]()
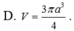
Trong không gian cho tam giác ABC vuông cân tại A, ABa. Gọi H là trung điểm BC. Quay tam giác đó xung quanh trục AH, ta được một hình nón tròn xoay. Tính diện tích xung quanh
S
x
q
của hình nón.
Đọc tiếp
Trong không gian cho tam giác ABC vuông cân tại A, AB=a. Gọi H là trung điểm BC. Quay tam giác đó xung quanh trục AH, ta được một hình nón tròn xoay. Tính diện tích xung quanh S x q của hình nón.
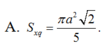
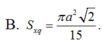
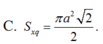
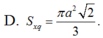
Cho tam giác đều ABC có diện tích là
3
quay xung quanh cạnh AC của nó. Tính thể tích V của khối tròn xoay được tạo thành.
Đọc tiếp
Cho tam giác đều ABC có diện tích là 3 quay xung quanh cạnh AC của nó. Tính thể tích V của khối tròn xoay được tạo thành.
![]()
![]()
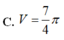
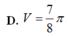
Cho tam giác ABC có
A
B
C
^
90
°
,
A
C
B
^
30
°
,
A
B
2
2
. Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có A B C ^ = 90 ° , A C B ^ = 30 ° , A B = 2 2 . Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:

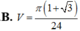
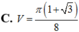
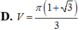
Trong không gian, cho tam giác ABC vuông tại A, ABa,
A
C
B
⏜
60
0
. Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Tính diện tích xung quanh
S
x
q
của hình tròn xoay đó.
Đọc tiếp
Trong không gian, cho tam giác ABC vuông tại A, AB=a, A C B ⏜ = 60 0 . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Tính diện tích xung quanh S x q của hình tròn xoay đó.
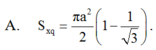
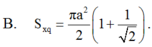
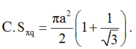
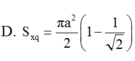
Trong không gian, cho tam giác ABC vuông tại A, ABa, ABC60
°
. Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Diện tích xung quanh của hình tròn xoay đó bằng
Đọc tiếp
Trong không gian, cho tam giác ABC vuông tại A, AB=a, ABC=60 ° . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Diện tích xung quanh của hình tròn xoay đó bằng