Các câu hỏi tương tự
Cho hai vecto
a
→
và
b
→
đều khác vecto
0
. Hãy xác định vecto
c
→
2
a
→
-
b
→
và giải thích tại sao ba vecto
a
→
,
b...
Đọc tiếp
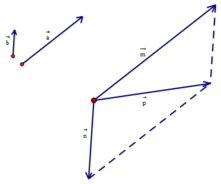
Cho hai vecto a → và b → đều khác vecto 0 . Hãy xác định vecto c → = 2 a → - b → và giải thích tại sao ba vecto a → , b → , c → đồng phẳng
Cho ba vecto
a
→
,
b
→
,
c
→
trong không gian. Chứng minh rằng nếu
m
a
→
+
n
b
→
+
p
c
→
0...
Đọc tiếp
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Cho ba vecto
n
→
,
a
→
,
b
→
bất kì đều khác với vecto
0
→
. Nếu vecto
n
→
vuông góc với cả hai vecto
a
→
v
à
b
→
thì
n
→
,
a
→
v
à...
Đọc tiếp
Cho ba vecto n → , a → , b → bất kì đều khác với vecto 0 → . Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có giá vuông góc với nhau từng đôi một
D. có thể đồng phẳng
Cho vecto
n
→
≠
0
→
và hai vecto
a
→
v
à
b
→
không cùng phương. Nếu vecto
n
→
vuông góc với cả hai vecto
a
→
v
à
b
→
thì
n
→
,
a
→...
Đọc tiếp
Cho vecto n → ≠ 0 → và hai vecto a → v à b → không cùng phương. Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có thể đồng phẳng
D. có thể không đồng phẳng
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.Vecto
A
C
→
cùng với hai vecto nào sau đây là ba vecto không đồng phẳng? A.
A
B
→
v
à
A
D
→
B.
M...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto A C → cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?
A. A B → v à A D →
B. M N → v à A D →
C. Q M → v à B D →
D. Q P → v à C D →
Cho hai vecto
a
→
và
b
→
không cùng phương. Hai vecto nào sau đây cùng phương? A. B. C. D.
Đọc tiếp
Cho hai vecto a → và b → không cùng phương. Hai vecto nào sau đây cùng phương?
A. 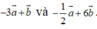
B. 
C. 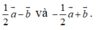
D. 
Cho hai vecto
a
→
và
b
→
không cùng phương. Hai vecto nào sau đây là cùng phương? A. B. C. D.
Đọc tiếp
Cho hai vecto a → và b → không cùng phương. Hai vecto nào sau đây là cùng phương?
A. ![]()
B. 
C. 
D. 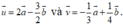
Cho các mệnh đề sau: (I) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng cùng nằm trong một mặt phẳng. (II) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng có giá song song với một mặt phẳng. (III) 3 vecto
a
⇀
,
b
⇀
,
c
⇀
đồng phẳng nếu tồn tại duy nhất bộ số (m,n) sao cho
a
⇀
...
Đọc tiếp
Cho các mệnh đề sau:
(I) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng cùng nằm trong một mặt phẳng.
(II) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng có giá song song với một mặt phẳng.
(III) 3 vecto a ⇀ , b ⇀ , c ⇀ đồng phẳng nếu tồn tại duy nhất bộ số (m,n) sao cho a ⇀ = m b ⇀ + n c ⇀ .
Số mệnh đề đúng là:
A. 0
B. 1
C. 2
D. 3
Cho điểm M(-4;2) và vecto v =(3;-1). Tìm điểm N biết M là ảnh của N qua phép tịnh tiến theo vecto v.