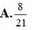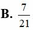Các câu hỏi tương tự
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y
∈
ℤ
) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là . A.
1
B.
8
21
C.
7
21
D.
13
21
Đọc tiếp
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y ∈ ℤ ) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là .
A. 1
B. 8 21
C. 7 21
D. 13 21
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm A(-2; 0), B(-2; 2), C(4; 2), D(4;0). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên( tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x; y) mà x + y 2. A.
3
7
.
B.
8
21
....
Đọc tiếp
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm A(-2; 0), B(-2; 2), C(4; 2), D(4;0). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên( tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x; y) mà x + y < 2.
A. 3 7 .
B. 8 21 .
C. 1 3 .
D. 4 7 .
Trên mặt phẳng
O
x
y
ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0) (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y 2 A.
1...
Đọc tiếp
Trên mặt phẳng O x y ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0) (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y < 2
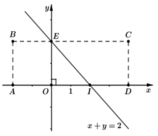
A. 1 3
B. 8 21
C. 3 7
D. 4 7
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;1;0) ,N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với
x
,
y
∈
ℤ
nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A(x;y). Xác suất để
x
+
y
≤...
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;1;0) ,N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x , y ∈ ℤ nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A(x;y). Xác suất để x + y ≤ 90 bằng
A. 845 1111
B. 473 500
C. 169 200
D. 86 101
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y), (x, y
∈
Z) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)
∈
S. Xác suất để x + y
≤
90 bằng
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y), (x, y ∈ Z) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y) ∈ S. Xác suất để x + y ≤ 90 bằng
![]()
![]()
![]()
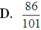
Gọi S là tập hợp tất cả các điểm M(x;y) có tọa độ là các số nguyên thỏa mãn
0
≤
x
≤
4
;
0
≤
y
≤
4
. Chọn ngẫu nhiên 3 điểm thuộc S. Xác suất để ba điểm được chọn là ba đỉnh một tam giác bằng
Đọc tiếp
Gọi S là tập hợp tất cả các điểm M(x;y) có tọa độ là các số nguyên thỏa mãn 0 ≤ x ≤ 4 ; 0 ≤ y ≤ 4 . Chọn ngẫu nhiên 3 điểm thuộc S. Xác suất để ba điểm được chọn là ba đỉnh một tam giác bằng
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy , cho hình bình hành ABCD với A(3;2) ; D(4;1). Biết điểm B di động trên đường tròn (C):(x-2)^2+(y+1)^2=32 điểm C thuộc đường thẳng (d):x+y-1=0 .Biết rằng C có hoành độ dương . Tọa độ điểm C là
Trong mặt phẳng với hệ tọa độ Oxy, chọn ngẫu nhiên một điểm mà tọa độ là các số nguyên có giá trị tuyệt đối nhỏ hơn hay bằng 4. Nếu các điểm có cùng xác suất được chọn như nhau, vậy thì xác suất để chọn được một điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là: A.
13
81
B.
15
81
C.
13
32
D. ...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, chọn ngẫu nhiên một điểm mà tọa độ là các số nguyên có giá trị tuyệt đối nhỏ hơn hay bằng 4. Nếu các điểm có cùng xác suất được chọn như nhau, vậy thì xác suất để chọn được một điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là:
A. 13 81
B. 15 81
C. 13 32
D. 11 16
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x - y + 1 0 và x + y - 4 0. Phương trình đường thẳng AD là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x - y + 1 = 0 và x + y - 4 = 0. Phương trình đường thẳng AD là
![]()
![]()
![]()
![]()