Chọn D
Giả sử z = x + yi (x, y ∈ R) là một nghiệm của phương trình.
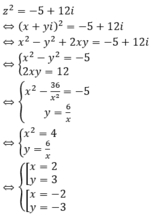
Do đó phương trình có hai nghiệm là z = - 2 - 3 i h o ặ c z = 2 + 3 i
Chọn D
Giả sử z = x + yi (x, y ∈ R) là một nghiệm của phương trình.
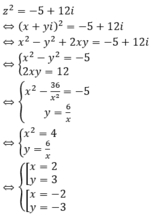
Do đó phương trình có hai nghiệm là z = - 2 - 3 i h o ặ c z = 2 + 3 i
Phương trình z 3 - ( 1 + i ) z 2 + ( 3 + i ) z - 3 i = 0 có tập nghiệm là:
A. 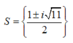
B. 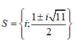
C. 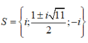
D. 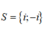
Cho các số phức z 1 = 1 , z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z − z i + z − z 2 . Tính tổng
A. S = 4 + 2 5 .
B. S = 5 + 17 .
C. S = 1 + 10 + 17 .
D. S = 10 + 2 5 .
Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.
A. 2,01.
B. 2, 03.
C. 2,05.
D. 2,06.
Số phức z nào dưới đây thỏa mãn (2-i) z 2 + ( 4 + 3 i ) z - 5 ( 1 - i ) = 0 ?
A. z = i
B. z = 1 + i
C. z = 1 - i
D. z = 1
Cho số phức z thỏa mãn z - 3 + 3 i = 2 . Giá trị lớn nhất của z - i là
A. 7
B. 9
C. 6
D. 8
Giải các phương trình sau: (1+3i)z-(2+5i)=(2+i)z
Số phức z nào dưới đây là nghiệm của phương trình: ( - 1 + i ) z 4 - 3 ( 2 - i ) z 2 + ( 16 i + 2 ) = 0
A. z = i
B. z = -i
C. z = i + 1
D. z = 5
Có bao nhiêu số phức z thỏa mãn z 2 = 2 z + z ¯ và z - 1 - i = z - 3 + 3 i ?
A. 4
B. 3
C. 1
D. 2
Phương trình z 1 = 1 + 2 i , z 2 = 2 - 3 i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Có bao nhiêu số phức z thỏa mãn z 2 = 2 z + z ¯ + 4 và |z-1-i|=|z-3+3i|?
A. 4.
B.3.
C. 1.
D. 2