Chọn D.
Theo giả thiết ta có:
z2 - 2z + 1 - 2i = 0 hay ( z - 1) 2 = 2i
suy ra z – 1 = ±( 1 + i)
z = 2 + i hoặc z = -i
Vậy chọn D.
Chọn D.
Theo giả thiết ta có:
z2 - 2z + 1 - 2i = 0 hay ( z - 1) 2 = 2i
suy ra z – 1 = ±( 1 + i)
z = 2 + i hoặc z = -i
Vậy chọn D.
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z3=1+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
![]()
![]()
![]()
![]()
Cho phương trình z 2 + b z + c = 0 có hai nghiệm z 1 ; z 2 thỏa mãn z 2 - z 1 = 4 + 2 i . Gọi A, B là điểm biểu diễn các nghiệm của phương trình z 2 - 2 b z + 4 c = 0 . Tính độ dài đoạn AB
A. 8 5
B. 2 5
C. 4 5
D. 5
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2 i .Tích của hai số b và c bằng
A. 3
B.-10
C.-2 và 5
D. 5
Biết rằng phương trình z 2 + b z + c = 0 , b , c ∈ R có một nghiệm phức là z 1 = 1 + 2 i .
Khi đó b+c ?
A. b+c = 2
B. b+c = 3
C. b+c = 0
D. b+c = 7
Biết rằng phương trình z 2 + bz + c = 0(b,c ∈ ℝ ) có một nghiệm phức là z 1 = 1 + 2i. Khi đó
A. b + c = 0
B. b + c = 3
C. b + c = 2
D. b + c = 7
Cho số phức w, biết rằng z 1 = w - 2 i và z 2 = 2 w - 4 là hai nghiệm của phương trình z 2 + a z + b = 0 với a, b là các số thực. Tính z 1 + z 2
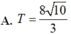
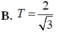
![]()
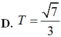
Cho z1; z2; z3; z4 là các nghiệm của phương trình: (z2 +1) (z2 - 2z + 2) = 0 . Tính ![]()
A.5
B.4
C.-2
D.3
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4