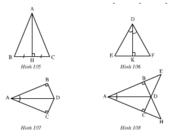
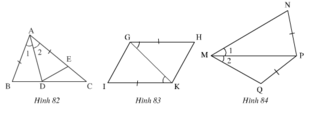
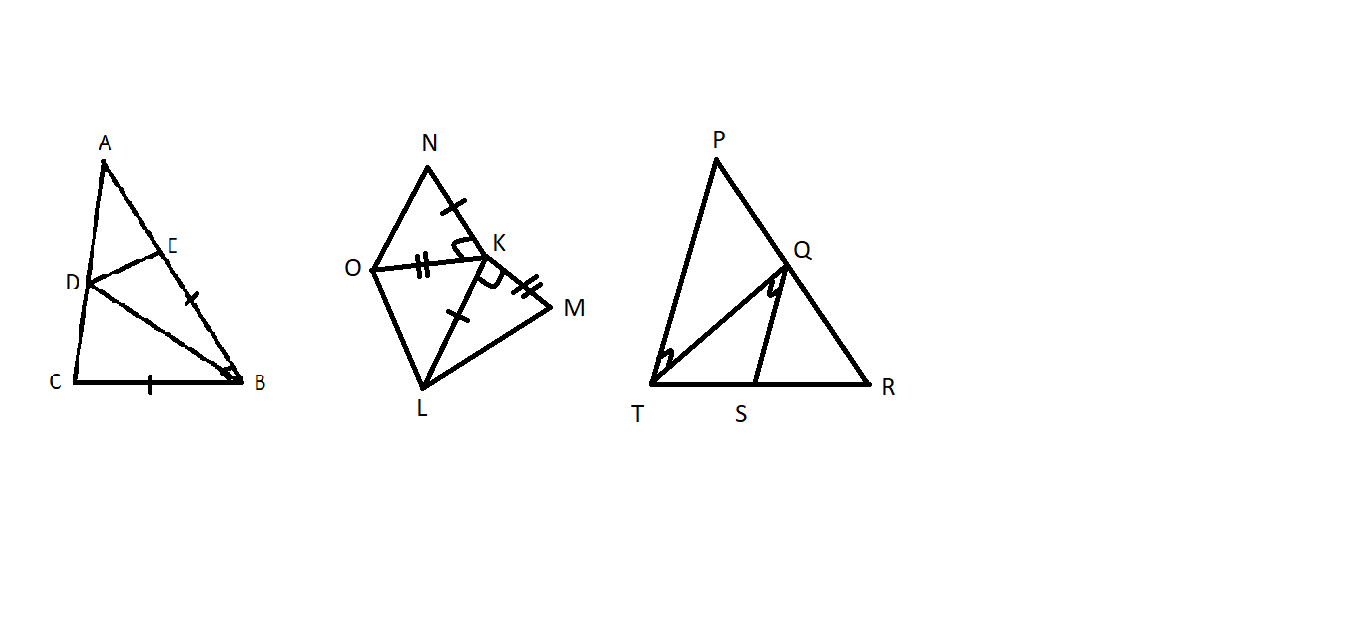
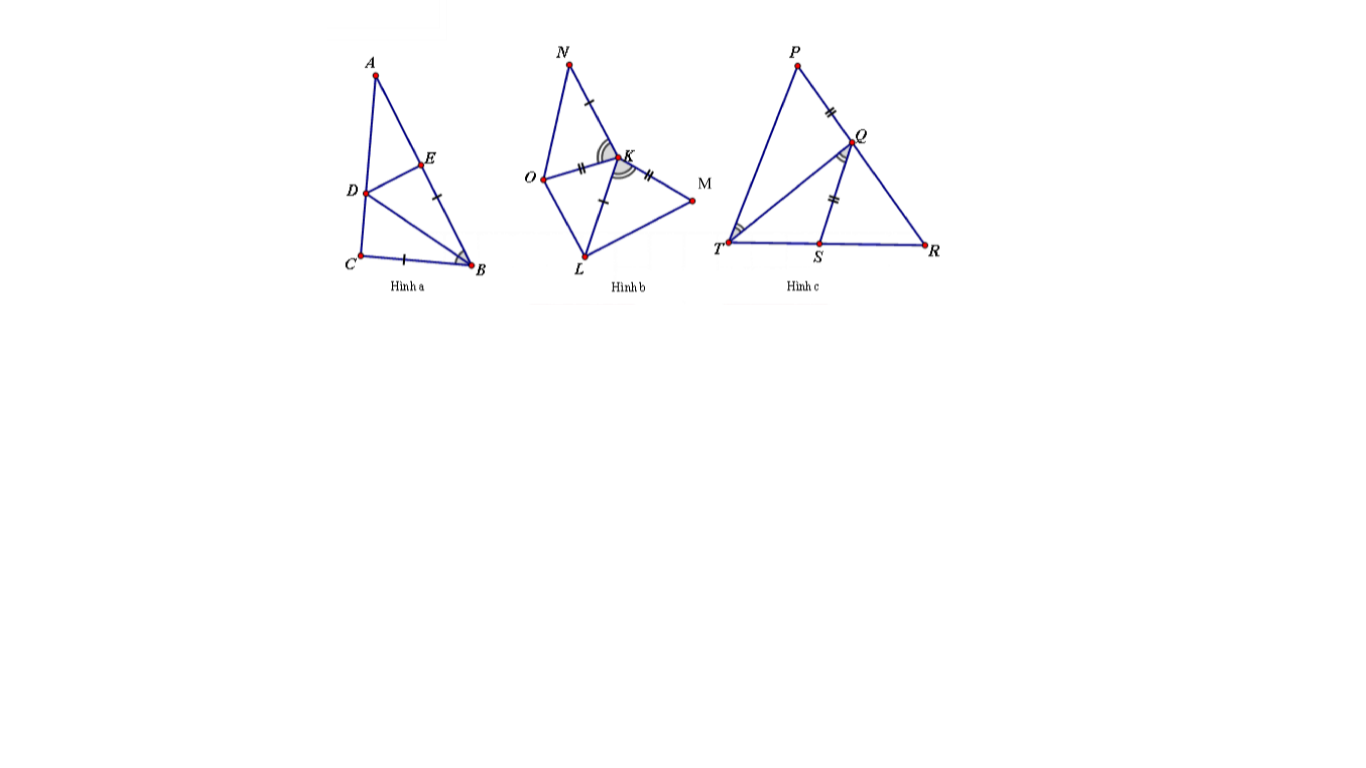
Hình 105
∆ABHvà ∆ACH có:
BH=CH(gt)
=
(góc vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(g.c.g)
Hình 106
∆DKE và ∆DKF có:
=
(gt)
DK là cạnh chung.
=
(góc vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107
Ta có:
∆ABD=∆ACD(g.c.g)
(Cạnh huyền góc nhọn).
Hình 108
Ta có:
∆ABD=∆ACD(Cạnh huyền - góc nhọn)
∆DBE=∆ACH(g.c.g)
∆ABH=ACE (g.c.g)
Hoàng Xuân Hải
∆ABHvà ∆ACH có:
BH=CH(gt)
\(\widehat{ABH}=\widehat{AHC}\)(góc vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(g.c.g)
Hình 106
∆DKE và ∆DKF có:
\(_{\widehat{EDK}=\widehat{FDK}}\)(gt)
DK là cạnh chung.
\(_{\widehat{DKE}=\widehat{DKF}}\)(góc vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107
Ta có:
∆ABD=∆ACD(g.c.g)
(Cạnh huyền góc nhọn).
Hình 108
Ta có:
∆ABD=∆ACD(Cạnh huyền - góc nhọn)
∆DBE=∆ACH(g.c.g)
∆ABH=ACE (g.c.g)
Hình 105:
AHB = AHC
Hình 106 :
DKE = DKF
Hình 107:
BAD = CAD
Hình 108:
ABD = ACD
BED = CHD
Giải:
Hình 105
∆ABH và ∆ACH có:
BH = CH(gt)
\(\widehat{AHB}\)=\(\widehat{AHC}\)(góc vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(g.c.g)
Hình 106
∆DKE và ∆DKF có:
\(\widehat{EDK}\)= \(\widehat{FDK}\)(gt)
DK là cạnh chung.
\(\widehat{DKE=}\)\(\widehat{DKF}\)(góc vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107
Ta có:
∆ABD=∆ACD(g.c.g)
(Cạnh huyền góc nhọn).
Hình 108
Ta có:
∆ABD=∆ACD(Cạnh huyền - góc nhọn)
∆DBE=∆ACH(g.c.g)
∆ABH=ACE (g.c.g)
Giải:
Hình 105
∆ABH và ∆ACH có:
BH = CH(gt)
$$=$$(góc vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(g.c.g)
Hình 106
∆DKE và ∆DKF có:
$$= $$(gt)
DK là cạnh chung.
$$$$(góc vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107
Ta có:
∆ABD=∆ACD(g.c.g)
(Cạnh huyền góc nhọn).
Hình 108
Ta có:
∆ABD=∆ACD(Cạnh huyền - góc nhọn)
∆DBE=∆ACH(g.c.g)
∆ABH=ACE (g.c.g)