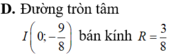Đặt z = x + yi. Từ |z – (3 – 4i)| = 2 suy ra:
( x - 3 ) 2 + ( y + 4 ) 2 = 4
Các điểm biểu diễn z nằm trên đường tròn tâm I(3; -4) bán kính 2.
Đặt z = x + yi. Từ |z – (3 – 4i)| = 2 suy ra:
( x - 3 ) 2 + ( y + 4 ) 2 = 4
Các điểm biểu diễn z nằm trên đường tròn tâm I(3; -4) bán kính 2.
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2
(Đề thi Đại học năm 2009, khối D)
Trên mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – i| = |(1 + i)z|.
(Đề thi Đại học năm 2010, khối B)
Trên mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – i| = |(1 + i)z|.
(Đề thi Đại học năm 2010, khối B)
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - ( 3 - 4 i ) = 2
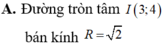
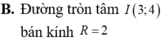
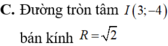
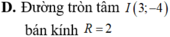
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện z - ( 3 - 4 i ) = 2
A. Đường tròn tâm I(3;4) R=12
B. Đường tròn tâm I(3;4) R=4
C. Đường tròn tâm I(3;-4) R=2
D. Đường tròn tâm I(3;4) R=8
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện log 2 z - 3 - 4 i = 1
A. Đường thẳng qua gốc tọa độ
B. Đường tròn bán kính 1
C. Đường tròn tâm I(3;-4) bán kính 2
D. Đường tròn tâm I(3;-4) bán kính 3
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z = z ¯ - 3 + 4 i là đường thẳng
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
A. Đường tròn ( x - 2) 2 + ( y + 2) 2 = 100.
B. Elip 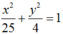
C. Đường tròn ( x -2) 2 + ( y + 2) 2 = 10.
D. Elip 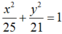
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z z + i = 3