a, HS tự chứng minh
b, M chính giữa A B ⏜
=> NE là phân giác B N A ^
=> B N A N = E B E A (tính chất đường phân giác) => BN.AE = NA.BE
c, HS tự chứng minh
d, Chứng minh ∆ABN:∆DBN => ĐPCM

a, HS tự chứng minh
b, M chính giữa A B ⏜
=> NE là phân giác B N A ^
=> B N A N = E B E A (tính chất đường phân giác) => BN.AE = NA.BE
c, HS tự chứng minh
d, Chứng minh ∆ABN:∆DBN => ĐPCM
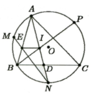
Cho đường tròn (O) lấy 3 điểm A,B, theo thứ tự gọi M,N,P lần lượt là điểm chính giữa của các cung AB,BC,CA. BP cắt AN tại I , MN cắt AB tại E .
a/ chứng minh tam giác BNI cân .
b/ chứng minh AE.BN=EB.AN
c/ chứng minh EI // BC.
d/ Gọi D là giao điểm của AN và BC . Chứng minh AN/BN = AB/BD
Trên đường tròn (O;R) lấy ba điểm A, B , C. Gọi M,N,P theo thứ tự là điểm chính giữa các cung AB, cung BC, cung AC, AN cắt BP tại I, AB cắt MN tại E. CMR
1) tam giác BNI cân
2) AE.BN = EB.AN
3) EI // BC
4) AN/BN = AB/BD với AN cắt BC tại D
cho đường tròn (o) và điểm A nằm ngoài đường tròn. vẽ cấc tiếp tuyến AB,AC với đường tròn (o) tại B và C.AO cắt đường tròn tại M và N (M nằm giữa A và O). Trên cung nhỏ MC lấy điểm D(D khác M và D khác C). AD cắt đường tròn tại điểm thứ hai là E. I là trung điểm của DE
a,Chứng minh A;B;I;O cùng thuộc một đương tròn
b,Gọi H là giao điểm của AO và BC. Chứng minh AM.AN=AH.AO
c,Qua D kẻ đường thẳng song song với AB cắt BC tại K.Chứng minh IK // BE
1. Cho các đường tròn (O;R) và (O';R') tiếp xúc trong với nhau tại A(R>R'). Vẽ đường kính AB của (O) , AB cắt (O') tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O'), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a) AP là phân giác của góc BAQ
b) CP và BR song song với nhau
2. Cho đường tròn (O;R) vơi SA là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). gọi I là trung điểm MA, K là giao điểm của BI với (O)
a) Chứng minh các tam giác IKA và IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB
b) Giả sử MK cắt (O) tại C. Chứng minh BC song song MA
3. Cho tam giác ABC nội tiếp đường tròn (O) và AB<AC. Đường tròn (I) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh OA và BD vuông góc với nhau.
4.Cho hai đường tròn (O) và (I) cắt nhau tại C và D, trong đó tiếp tuyến chung MN song song với cát tuyến EDF, M và E thuộc (O), N và F thuộc (I), D nằm giữa E và F. Gọi K ,H theo thứ tự là giao điểm của NC,MC và EF. Gọi G là giao điểm của EM ,FN. Chứng minh:
a) Các tam giác GMN và DMN bằng nhau
b) GD là đường trung trực của KH
Làm ơn giúp mình với !!! Chút nữa là mình đi học rồi !!!! Cảm ơn trước !!!
Cho đường tròn tâm o đường kính AB. Trên đường tròn lấy một điểm I( I ko trùng vs A và B ). Tia phân giác của góc IAB cắt cung IB tại M. Lấy điểm C nằm giữa 2 điểm O và B. MC cắt đường tròn tại điểm thứ hai là E, EI cắt AM tại K
a. Chứng minh 4 điểm A,K,C,I nằm trên một đường tròn
b. Chứng minh CK song song BI
c. Từ C vẽ đường thẳng song song với AI cắt IE tại F. Gọi giao điểm của IE và AB là N. Chứng minh NB.NC = NE.NF
Cho tam giác nhọn ABC ( AB<AC) nội tiếp đường tròn (O). Gọi E là điểm chính giữa của cung nhỏ BC. Trên cạnh AC lấy điểm M sao cho EM=EC, đường thẳng BM cắt đường tròn (O) tại N ( N khác B). Các đường thẳng EA và EN cắt cạnh BC lần lượt tại D và F.
a) Chứng minh tam giác AEN đồng dạng với tam giác FED
b) Chứng minh M là trực tâm của tam giác AEN
c) Gọi I là trung điểm của AN, tia IM cắt đường tròn (O) tại K. Chứng minh đường thẳng CM là tiếp tuyến của đường tròn ngoại tiếp tam giác BMK
Trên đường tròn (O) lấy ba điểm A, B và C. Gọi M, N và P theo thứ tự là điểm chính giữa của các cung AB, BC và AC. Gọi I là giao điểm của AB và MN. Gọi K là giao điểm của AN và PB. Chứng minh rằng:
a) Tam giác BNK cân. b) IA.IB = IM.IN c) AI.BN = IB.AN
Bài 1: Cho đường tròn (O) lấy 3 điểm A, B, C. Gọi D, E, F theo thứ tự là điểm chính giữa của các cung AB(không chứa C), BC (không chứa A), CA(không chứa B). Gọi G và I lần lượt là giao điểm của AE với BF và BC, H là giao điểm của AB và DE. Chứng minh rằng
a)HA.EB=HB.EA
b)HG song song với BC
c)AE/BE=AB/BI
Bài 2: Cho tam giác ABC, phân giác AD. Vẽ đường tròn (O) qua A và tiếp xúc với BC tại D cắt các cạnh AB, AC lần lượt ở E và F. Chứng minh rằng
a)EF//BC
b)AB.BE=BD^2
c)Tam giác ADF đồng dạng với tam giác ABD
d)AD^2=AC.AE
cho đường tròn (O;R) có BC là dây cố định (BC<2R) ; E là điểm chính giữa cung nhỏ BC. gọi A là điểm di động trên cung lớn BC và AB<AC (A khác B). trên đoạn AC lấy điểm D khác C sao cho ED=EC. tia BD cắt đường tròn (O;R) tại điểm thứ hai là F.
a) chứng minh D là trực tâm của tam giác AEF.
b) gọi H là trực tâm tam giác DEC ; DH cắt BC tại N. đường tròn ngoại tiếp tam giác BDN cắt đường tròn (O;R) tại điểm thứ hai là M. chứng minh đường thẳng DM luôn đi qua một điểm cố định.