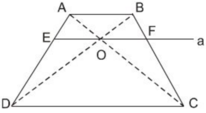
Trên đường chéo AC của hình vuông ta lấy một điểm E (E ≠ A,C). Đường thẳng qua E và song song với AB cắt AD và BC theo thứ tự tại các điểm Q, N. Đường thẳng qua E và song song với BC cắt AB và CD theo thứ tự tại P, M.
a) Chứng minh tứ giác MNPQ là hình thang cân.
b) So sánh SMNPQ và SABCD.
c) Xác định vị trí của E để hình thang MNPQ có chu vi nhỏ nhất.
a) Chứng minh được MN//PQ (cùng vuông góc với AC). Chứng minh được MP = QN. Þ ĐPCM.
b) Ta có:
S M N E = 1 2 S M E N C , S N P E = 1 2 S P B N E , S P Q E = 1 2 S , A P E Q S M Q E = 1 2 S Q E M D ⇒ S M N P Q = 1 2 S A B C S .
c) Chu vi MNPQ = MN + PQ + NP + QM
= EC + AE + BE + ED = AC + BE + ED.
Trong tam giác BED, BE + ED ³ BD
Þ Chu vi MNPQ ≥ AC + BD
Þ E là tâm của hình vuông ABCD