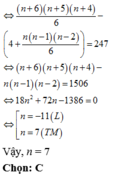Các câu hỏi tương tự
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247 A. 6 B. 7 C. 5 D. 8
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247
A. 6
B. 7
C. 5
D. 8
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3;4;5;6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
A. 781
B. 624
C. 816
D. 342
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt
(
n
≥
2
)
Biết rằng có 5700 tam giác có đỉnh là các điểm nói trên. Tìm giá trị của n A. 21 B. 30 C. 32 D. 20
Đọc tiếp
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt ( n ≥ 2 ) Biết rằng có 5700 tam giác có đỉnh là các điểm nói trên. Tìm giá trị của n
A. 21
B. 30
C. 32
D. 20
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n
≥
2) Biết rằng có 5700 tam giác có đỉnh là các điểm nói trên. Tìm giá trị của n A. 21 B. 30 C. 32 D. 20
Đọc tiếp
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n ≥ 2) Biết rằng có 5700 tam giác có đỉnh là các điểm nói trên. Tìm giá trị của n
A. 21
B. 30
C. 32
D. 20
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
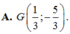
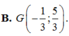
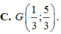
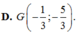
Cho đa giác (H) có n đỉnh
(
n
∈
ℕ
,
n
4
)
. Biết số các tam giác có 3 đỉnh là đỉnh của (H) và không có cạnh nào là cạnh của (H) gấp 5 lần số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H). Khẳng định nào sau đây đúng? A.
n
∈...
Đọc tiếp
Cho đa giác (H) có n đỉnh ( n ∈ ℕ , n > 4 ) . Biết số các tam giác có 3 đỉnh là đỉnh của (H) và không có cạnh nào là cạnh của (H) gấp 5 lần số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H). Khẳng định nào sau đây đúng?
A. n ∈ 4 ; 12
B. n ∈ 13 ; 21
C. n ∈ 22 ; 30
D. n ∈ 31 ; 38
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n
≥
2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n? A. 20 B. 21 C. 30 D. 32
Đọc tiếp
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n ≥ 2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 20
B. 21
C. 30
D. 32
Cho hai đường thẳng
d
1
và
d
2
song song với nhau. Trên
d
1
có 10 điểm phân biệt, trên
d
2
có n điểm phân biệt (
n
≥
2
). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n? A. 16 B. 21 C. 30 D. 20
Đọc tiếp
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt ( n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 16
B. 21
C. 30
D. 20