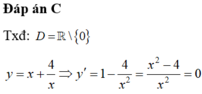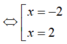Các câu hỏi tương tự
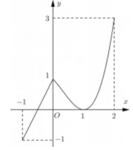
Cho hàm số y = f(x) liên tục trên đoạn [-1;2] và có đồ thị như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [-1;2] bằng
A. 1.
B.3.
C.0.
D. 2.
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
+
3
-
x
ln
x
trên đoạn [1;2] là: A. B. C. D.
Đọc tiếp
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + 3 - x ln x trên đoạn [1;2] là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây đúng?
A. m > 10
B. 8 < m < 10
C. 0 < m < 4
D. 4 < m < 8
Cho hàm số y f(x) nghịch biến trên
ℝ
và thỏa mãn [f(x) - x]f(x)
x
6
+
3
x
4
+
2
x
2
,
∀
x
∈
ℝ
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng A. 4 B. -28 C. -3 D. 33
Đọc tiếp
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
+
3
-
x
ln
x
trên đoạn [1;2] là: A. B. C. D.
Đọc tiếp
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + 3 - x ln x trên đoạn [1;2] là:
A. ![]()
B.![]()
C. ![]()
D. ![]()
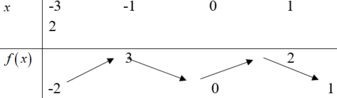
Cho hàm số y=f(x) liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2]. Tính M + m.
A. 3
B. 2
C. 1
D. 4
Cho hàm số
y
x
4
-
4
x
2
+
3
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
-
1
;
2
. Giá trị của
M
+
m
là
Đọc tiếp
Cho hàm số y = x 4 - 4 x 2 + 3 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn - 1 ; 2 . Giá trị của M + m là
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
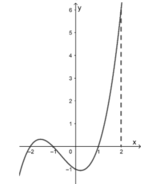
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Gọi M,N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 3 - 3 x 2 + 1 trên đoạn [1;2]. Khi đó tổng M+N bằng
A. 2.
B. – 2.
C. 0.
D. – 4.