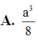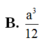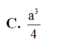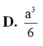Chọn B.
Gọi cạnh của hình lập phương là a, theo đề bài ra
![]()
![]()
Chọn B.
Gọi cạnh của hình lập phương là a, theo đề bài ra
![]()
![]()
Biết rằng thể tích của một khối lập phương bằng 8. Tính tổng diện tích các mặt của hình lập phương đó.
A. 16
B. 24
C. 36
D. 27.
Tổng diện tích các mặt của một khối lập phương là 54 c m 2 Tính thể tích của khối lập phương đó
A. 27 c m 3
B. 9 c m 3
C. 81 c m 3
D. 18 c m 3
Tổng diện tích các mặt của một hình lập phương là 96 c m 2 Thể tích của hình lập phương đó là:
A. 27 c m 3
B. 125 c m 3
C. 8 c m 3
D. 64 c m 3
Một khối rubik có hình lập phương (mỗi mặt của rubik có 9 ô vuông) có thể tích bằng 125 c m 3 . Hỏi tổng diện tích các mặt của khối rubik đó bằng bao nhiêu?
A. 150 c m 2
B. 25 c m 2
C. 54 c m 2
D. 108 c m 2
Diện tích một mặt của hình lập phương là 9. Thể tích khối lập phương đó là:
A. 729.
B. 81.
C. 27.
D. 9.
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?
A. 2
B. 8
C. 4
D. 6
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó: