Thế x = 1 + t y = 2 + 2 t vào (C) ta có:
(1+ t) 2+ (2+ 2t) 2-2( 1+t) -2 (2+ 2t) +1= 0
=> 5(t+1)2- 6 (1+ t) +1 = 0
=> 1 + t = 1 1 + t = 1 5 ; => [ t = 0 t = - 4 5
Với t= 0; (x; y) = ( 1;2) .
Với t= - 4 5 ; ( x ; y ) = 1 5 ; 2 5
Chọn B.
Thế x = 1 + t y = 2 + 2 t vào (C) ta có:
(1+ t) 2+ (2+ 2t) 2-2( 1+t) -2 (2+ 2t) +1= 0
=> 5(t+1)2- 6 (1+ t) +1 = 0
=> 1 + t = 1 1 + t = 1 5 ; => [ t = 0 t = - 4 5
Với t= 0; (x; y) = ( 1;2) .
Với t= - 4 5 ; ( x ; y ) = 1 5 ; 2 5
Chọn B.
Tìm tọa độ giao điểm của đường thẳng (d): \(\left\{{}\begin{matrix}x=2+t\\y=-1+3t\end{matrix}\right.\) (t ∈ R) với đường tròn (C):x2+y2-2x-1=0
Tìm tọa độ giao điểm của đường thẳng d: x- 2y + 3= 0 và đường tròn (C): x2+ y2- 2x – 4y = 0
A. (3; 3) và (-1; 1)
B. (1;1) và (-3;3)
C. (3; -3)
D. Đáp án khác
Trong mặt phẳng với hệ tọa độ cho đường tròn hai đường tròn (C): x2+ y2- 2x -2y +1= 0 và (C’) : x2+ y2+ 4x -5 = 0 cùng đi qua M( 1;0) .Viết phương trình đường thẳng d qua M cắt hai đường tròn lần lượt tại A; B sao cho MA= 2 MB.
A. 6x+ 6+ y= 0 hoặc -6x+ y- 6= 0
B. 2x+ 3y + 6= 0 hoặc 3x-2y + 3= 0
C. 2x+ y- 6= 0 hoặc x+ y- 6 = 0
D. 6x+ y – 6= 0 hoặc 6x –y-6= 0
Bài 7. Trong mặt phẳng Oxy, cho A(1;-2), B(2;3), C(-2;1) và D(2;-3m).
Tìm tọa độ giao điểm của AB với đường thẳng d: y = 3x-9.
Tọa độ giao điểm của đồ thị hai hàm số y = x2 - 2x +3 và y = x2 + 2x -1
A.(1;2) B.(0;4) C.(-1;6) D.(-1;-2 )
Câu 14(1,5 điểm): a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = - 2x + 5 ; y = x + 2 b) Tìm tọa độ giao điểm A của đường thẳng y = - 2x + 5 và y=x+2. c) Tính góc tạo bởi đường thẳng y = x + 2y với trục Ox. d) Xác định đường thẳng y = ax + b đi qua điểm A và song song với đường thẳng y = - 3x - 1
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1= 0 và đường thẳng d: x+ y+1= 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
![]()
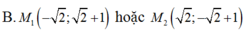
![]()
![]()
Viết phương trình đường thẳng (△):
a) đi qua M(1;2), vtcp u=(3;-4)
b) đi qua M(-2;4), vtpt n=(2;3)
c) đi qua 2 điểm A(-2;1); B(3;2)
d) đi qua M(4;-2), song song d: 3x-5y+7=0
e) đi qua N(1;-3), song song d: \(\left\{{}\begin{matrix}x-1-3t\\y=2+t\end{matrix}\right.\)
f) đi qua P(3;5), vuông góc (d): 2x-7y-1=0
g) đi qua Q(-2;0), vuông góc (d): \(\left\{{}\begin{matrix}x=2+5t\\y=1-t\end{matrix}\right.\)
h) đi qua I(1;-1) và tạo (d): x-3y+7=0 một góc α=\(\dfrac{\sqrt{2}}{10}\)
l) đi qua J(1;-1) và cách điểm K(2;3) một khoảng là \(\dfrac{19}{5}\)
cho đường thẳng d:x+y+2=0 và đường tròn (C): x^2+y^2-4x-2y=0. Gọi I là tâm đường tròn (C), M là điểm thuộc d. qua M kẻ tiếp tuyến MA với (C) và 1 cát tuyến cắt (C) tại B,C. Tìm tọa độ điểm M biết tam giác ABc vuông tại B và có diện tích bằng 5