Đáp án B.
Hoành độ giao điểm của (C) và (d) là nghiệm của phương trình

Hoành độ nhỏ hơn 1 nên ta chọn x = 0 => y = 1. Vậy tọa độ điểm cần tìm là A(0;1).
Đáp án B.
Hoành độ giao điểm của (C) và (d) là nghiệm của phương trình

Hoành độ nhỏ hơn 1 nên ta chọn x = 0 => y = 1. Vậy tọa độ điểm cần tìm là A(0;1).
Trong không gian Oxyz, cho điểm A(1;2;-1), đường thẳng d: x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P):x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-1), đường thẳng d : x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P): x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Trong không gian với hệ tọa độ oxyz, cho mặt phẳng (P): x+y+z-3=0 và đường thẳng d : x - 2 1 = y + 1 - 2 = z - 1 . Gọi I là giao điểm của mặt phẳng (P) với đường thẳng d. Điểm M thuộc mặt phẳng (P) có hoành độ dương sao cho IM vuông góc với d và I M = 4 14 có tọa độ là:
![]()
![]()
![]()
![]()
Điểm E(4;5;5), mặt phẳng (P): x-2y+2z+6=0 và đường thẳng d : x + 1 2 = y - 3 - 1 = z - 2 1 . Tìm tọa độ điểm M có hoành độ nhỏ hơn 2 nằm trên đường thẳng d có khoảng cách từ M tới mặt phẳng (P) bằng EM.
![]()
![]()
![]()
![]()
Tọa độ điểm M có hoành độ nguyên thuộc đồ thị (C) của hàm số y = x + 2 x - 1 có khoảng cách đến đường thẳng
d: x - y +1 = 0 bằng 1 2 là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Cho đường thẳng d : x - 1 2 = y + 1 - 1 = z 1 và các điểm A(1;-1;2), B(2;-1;0). Tìm tọa độ điểm M thuộc đường thẳng d sao cho tam giác AMB vuông tại M
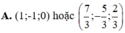
![]()
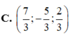
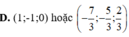
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : x + 1 2 = y 1 = z - 2 1 mặt phẳng (P): x+y-2z+5=0 và A(1;-1;2) Đường thẳng ∆ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN . Một vectơ chỉ phương của ∆ là:
A. u → = ( 2 ; 3 ; 2 )
B. u → = ( 1 ; - 1 ; 2 )
C. u → = ( - 3 ; 5 ; 1 )
D. u → = ( 4 ; 5 ; - 13 )
Tìm tọa độ giao điểm M của đường thẳng d:\(\left\{{}\begin{matrix}x=1+2t\\y=-2-t\\z=1-t\end{matrix}\right.\)và (P) :4x-y-z+5=0
A. M(1;1;2)
B. M(1;-1;2)
C. M(1;1;-2)
D. M(-1;-1;2)