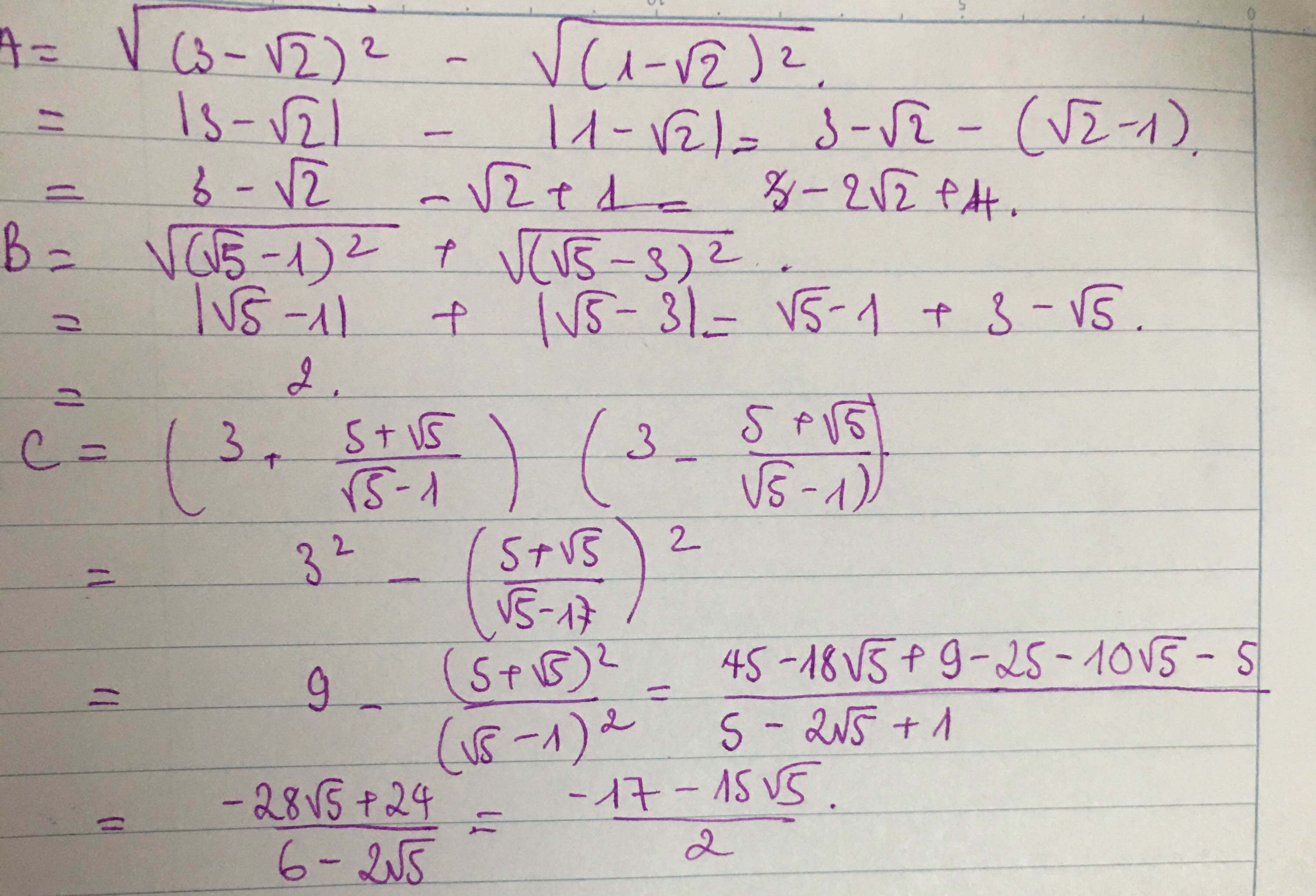A = \(\sqrt{\left(3-\sqrt{2}\right)^2-\sqrt{\left(1-\sqrt{2}\right)^2}}\)
\(A=3-\sqrt{2}-\sqrt{\left(1-\sqrt{2}\right)^2}\)
\(A=3-\sqrt{2}-\left(-\left(1-\sqrt{2}\right)\right)\)
\(A=3-\sqrt{2}+1-\sqrt{2}\)
\(A=4-\sqrt{2}-\sqrt{2}\)
\(A=4-2\sqrt{2}\)
\(B=\sqrt{\left(\sqrt{5}-1\right)^2}+\sqrt{\left(\sqrt{5}-3\right)^2}\)
\(B=\sqrt{5}-1+\sqrt{\left(\sqrt{5}-3\right)^2}\)
\(B=\sqrt{5}-1-\left(\sqrt{5}-3\right)\)
\(B=\sqrt{5}-1-\sqrt{5}+3\)
\(B=-1+3\)
\(B=2\)
\(C=\left(3+\dfrac{5+\sqrt{5}}{\sqrt{5}-1}\right)\left(3-\dfrac{5+\sqrt{5}}{\sqrt{5}-1}\right)\)
\(C=3^2-\left(\dfrac{5+\sqrt{5}}{\sqrt{5}-1}\right)^2\)
\(C=9-\left(\dfrac{5+\sqrt{5}}{\sqrt{5}-1}\right)^2\)
\(C=9-\left(\dfrac{5+\sqrt{5}}{\sqrt{5}-1}.\dfrac{\sqrt{5}+1}{\sqrt{5}+1}\right)^2\)
\(C=9-\left(\dfrac{\left(5+\sqrt{5}\right)\left(\sqrt{5}+1\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}\right)^2\)
\(C=9-\left(\dfrac{5\sqrt{5}+5.1+\sqrt{5}\sqrt{5}+\sqrt{5}.1}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}\right)\)
\(C=9-\left(\dfrac{5\sqrt{5}+5.1+\sqrt{5}\sqrt{5}+\sqrt{5}.1}{\left(\sqrt{5}\right)^2-1^2}\right)^2\)
\(C=9-\left(\dfrac{5\sqrt{5}+5.1+\sqrt{5.5}+\sqrt{5}.1}{\left(\sqrt{5}\right)^2-1^2}\right)\)
\(C=9-\left(\dfrac{5\sqrt{5}+5+\sqrt{25}+\sqrt{5}}{4}\right)^2\)
\(C=9-\left(\dfrac{5\sqrt{5}+5+5+\sqrt{5}}{4}\right)^2\)
\(C=9-\left(\dfrac{6\sqrt{5}+10}{4}\right)^2\)
\(C=9-\left(\dfrac{3\sqrt{5}+5}{2}\right)^2\)
\(C=9-\dfrac{\left(3\sqrt{5}+5\right)}{2^2}^2\)
\(C=9-\dfrac{30\sqrt{5}+70}{4}\)
\(C=9-\dfrac{15\sqrt{5}+35}{2}\)
\(C=\dfrac{-17-15\sqrt{5}}{2}\)