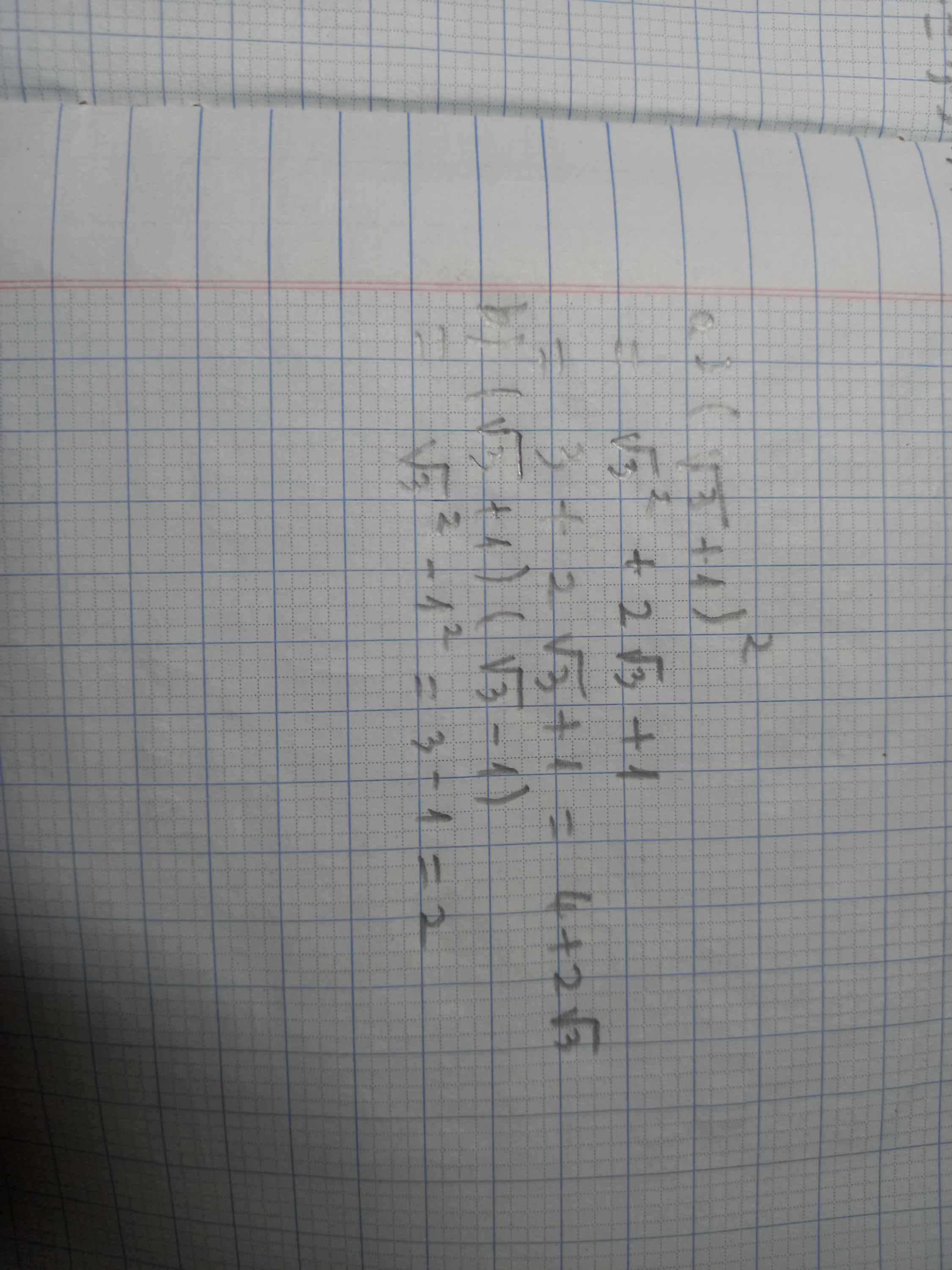Question

Tính:

\(a.\left(\sqrt{3}+1\right)^2\) \(b.\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)\)

Answer 1

a) \(\left(\sqrt{3}+1\right)^2=\sqrt{3}^2+2\sqrt{3}+1=4+2\sqrt{3}\)

b) \(\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=\sqrt{3}^2-1=2\)

Answer 2

`a)(\sqrt{3}+1)^2=(\sqrt{3})^2+2.\sqrt{3}.1+1^2=3+2\sqrt{3}+1=4+2\sqrt{3}`

`b)(\sqrt{3}+1)(\sqrt{3}-1)=(\sqrt{3})^2-1^2=3-1=2`

Answer 3

Answer 4

\(\left(\sqrt{3}+1\right)^2=3+2\sqrt{3}+1=4+2\sqrt{3}\)

\(\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=\left(\sqrt{3}\right)^2-1^2=3-1=2\)