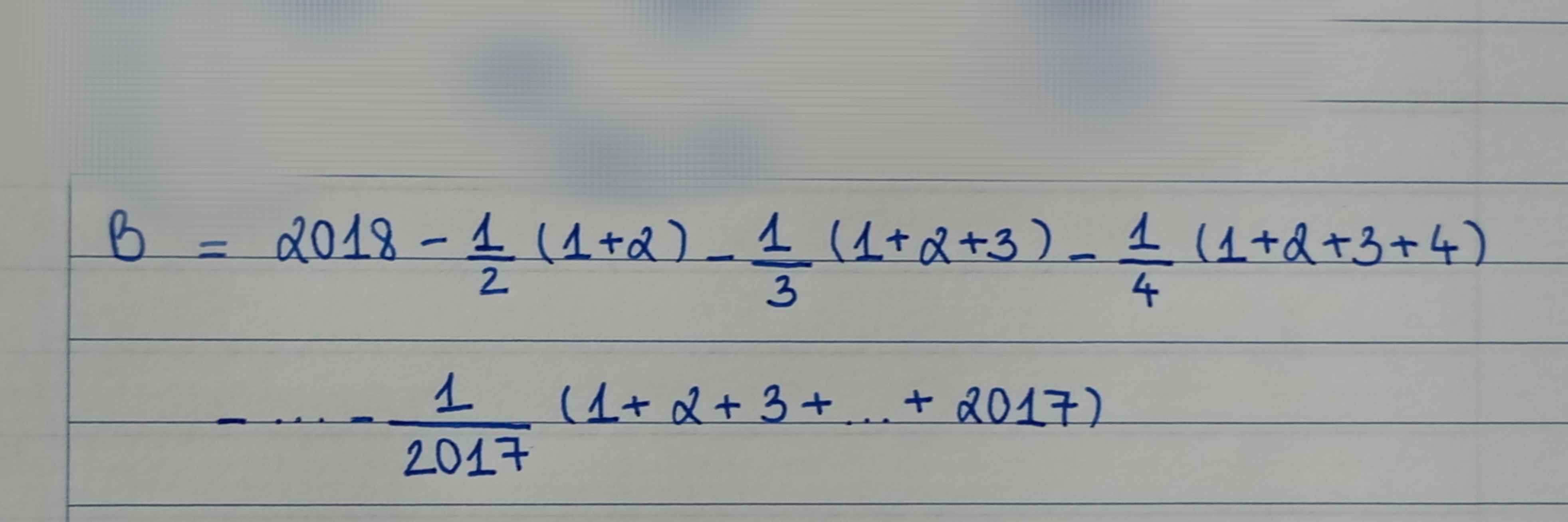\(B=2018-\dfrac{1}{2}\left(1+2\right)-\dfrac{1}{3}\left(1+2+3\right)-\dfrac{1}{4}\left(1+2+3+4\right)-...-\dfrac{1}{2017}\left(1+2+3+...+2017\right)\)
\(B=2018-\dfrac{2+1}{2}-\dfrac{3+1}{2}-\dfrac{4+1}{2}-...-\dfrac{2017+1}{2}\)
\(B=2018-\dfrac{3}{2}-\dfrac{4}{2}-\dfrac{5}{2}-...-\dfrac{2018}{2}\)
\(B=2018-\dfrac{3+4+5+...+2018}{2}\)
\(B=2018-\dfrac{\left(2018+3\right)\left(2018-3+1\right)}{2}:2\)
\(B=2018-\dfrac{2021.2016}{2}:2\)
\(B=2018-2021.1008:2\)
\(B=2018-1018584\)
\(B=-1016566\)
Đúng 2
Bình luận (0)
