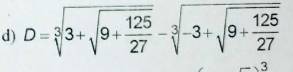\(D=\sqrt[3]{3+\sqrt{9+\dfrac{125}{27}}}-\sqrt[3]{-3+\sqrt{9+\dfrac{125}{27}}}\)
\(\Rightarrow D^3=\left(\sqrt[3]{3+\sqrt{9+\dfrac{125}{27}}}-\sqrt[3]{-3+\sqrt{9+\dfrac{125}{27}}}\right)^3\)
\(=3+\sqrt{9+\dfrac{125}{27}}+3-\sqrt{9+\dfrac{125}{27}}-3\sqrt[3]{3+\sqrt{9+\dfrac{125}{27}}}\sqrt[3]{-3+\sqrt{9+\dfrac{125}{27}}}\left(\sqrt[3]{3+\sqrt{9+\dfrac{125}{27}}}-\sqrt[3]{-3+\sqrt{9+\dfrac{125}{27}}}\right)\)
\(=6-3\sqrt[3]{9+\dfrac{125}{27}-9}.D\)
\(=6-3\sqrt[3]{\dfrac{125}{27}}.D\)
\(=6-5D\)
\(\Rightarrow D^3+5D-6=0\)
\(\Leftrightarrow\left(D-1\right)\left(D^2+D+6\right)=0\)
\(\Leftrightarrow D-1=0\) (vì \(D^2+D+6=\left(D^2+2.\dfrac{1}{2}.D+\dfrac{1}{4}\right)+\dfrac{23}{4}=\left(D+\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\))
\(\Leftrightarrow D=1\)
Vậy \(D=1.\)